Frame of Reference (Space and Time) | Inertial and non inertial Frames
Frame of Reference (Space and Time)
In order to describe the motion of a particle in space, we need to know its position at different instant of time. If we imagine a coordinate system attached to a rigid body and we describe the position of any particle relative to it, then such a coordinate system is called frame of reference. For the location of the objects, the position vectors are drawn from the origin O of the coordinate system. The simplest frame of reference is a coordinate system.
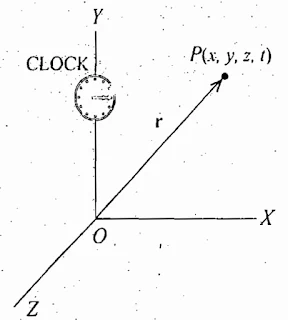 |
| Frame of Reference |
r = xi +yj + zk
In order to know the position of the particles at different instants of time, an observer may be stationed at the origin with a clock to measure the time t. Thus we obtain the position vector r of the particle as the function of the time t i.e.,
r = r (t)
The position and time recorded together constitute an event, represented by four coordinates (x, y, z, t) and the reference system, used for this purpose, may be called as space-time reference system.
Types of Frame of Reference
There are two types of frame of Reference :
Inertial Frames
The frames of reference are at rest or in uniform translatory motion relative to one another are inertia frames.
 |
| Inertial Frames of Refference |
All the frames of reference at rest (v = 0) and moving with constant velocity dv/dt = 0 are inertia frames. Consider two frames of reference S & S'. S' is moving with constant velocity v relative to S. Then initially (t = 0) both the frames co-inside. After time t, the position of the particle in both frames be r and r' then
r = r' + vt
r' = r - vt
dr'/dt = dr/dt - v
u' = u - v
du'/dt = du/dt
a' = a
i.e. the particle experience the same acceleration in both the frames. Thus an unaccelerated frame is inertial frame. In other words "An inertial frame is one in which Newton's first law is true".
Note : Newton's laws are not hold correct in an accelerated and rotating frames.
Non-inertial Frame
The frames with respect to which an unaccelerated body accelerate are called non inertial frame i.e. accelerated frames are called non-inertial frames.
 |
| Non-inertial Frame of Reference |
Consider two system S and S', the latter moving with an acceleration (a) related to the frame. If we consider the first frame to be Inertial, then second frame will be non inertial and vice-versa.
The force experienced by the particle due to acceleration of non inertial frame is called the fictitious force. If a is acceleration of non inertial frame, then fictitious force = -ma0.
Considered a particle of mass m having an acceleration a0 as observed from system S, then
F = mai
If this acceleration is observed from system S', thus the total force,
F' = m (ai - a0)
F' = mai - ma0
F' = Fi - ma0
Clearly additional force on particle due to acceleration pf frame S' is given by
FP = -ma0
It is the quantity required to correct the equation of force in the non-inertial frame in order to get the Newton's laws to work.

