Kepler's Laws of Planetary motion, Dedication
Kepler's Laws of Planetary motion
In astronomy, Kepler's laws of planetary motion, proposed by Johannes Kepler during the period of 1609 to 1619, describe the orbits of planets around the Sun. The motion of planets has been a subject of much interest for astronomers from very early times.
 |
| Kepler's Laws of Planetary motion |
In the above figure, the orbits are ellipses, with focal points F1 and F2 for the first planet and F1 and F3 for the second planet. The Sun is placed in focal point F1.
The two shaded sectors A1 and A2 have the same surface area and the time for planet 1 to cover segment A1 is equal to the time to cover segment A2. Kepler's laws of planetary motion are as follows :
(i) The Law of Elliptical Orbits (First Law)
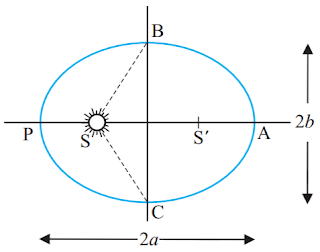
According to this law, "Every planet moves in an elliptical orbit around the sun, the sun being at one of the foci."
The point at which the planet is close to the sun is known as perihelion and the point at which the planet is farther from the sun is known as aphelion.
Dedication of Kepler's First Law
Let S be the sun (mass M) and a planet of mass m, revolving around the sun in elliptical orbit. The force acting between planet and sun is gravitational and given by
`F=-\frac{GMm}{r^{2}}\hat{r}`
r being position vector of planet relative to sun
`F=-\frac{GMm}{r^{3}}r=f(r)r`
`f(r)r=-\frac{GMm}{r^{3}}`
Torque acting on planet.
`τ=r\times F=r\times f(r)r`
`τ=f(r)r\times r=0`
As torque acting on planet is zero, the angular momentum of the planet relative to sun is conserved.
The angular momentum of planet relative to sun is
`J=r\times p=r\times mv=constant`
It follows that J, being constant, must be perpendicular to the plane containing position vector r and velocity v that is the orbit of the plane must lie in a plane.
(ii) The Law of Areas ( Second Law)
According to this law, "The radius vector, drawn from the sun to a planet, sweeps out equal areas in equal times i.e., the areal velocity of the radius vector is constant."
As the orbit is not circular, the planet’s kinetic energy is not constant in its path. It has more kinetic energy near perihelion and less kinetic energy near aphelion implies more speed at perihelion and less speed at aphelion.
Deduction of Kepler's Second Law
Let P be the instantaneous position of planet relative to sun. The position vector of P relative to sun is r. After time Δt, the planet is at Q, having position vector r+Δr such let Δr = PQ
The area swept out by radius SP in time Δt.
ΔA = Area of triangle PSP'
`ΔA=\frac{1}{2} r × Δr`
Area swept by radius vector per second or Areal velocity,
`\frac{dA}{dt}=\lim_{Δt \rightarrow 0}\frac{ΔA}{Δt}`
`\frac{dA}{dt}=\lim_{Δt \rightarrow 0}\frac{\frac{1}{2}r\timesΔr}{Δt}`
`\frac{dA}{dt}=\frac{1}{2}r\times\frac{dr}{dt}`
`\frac{dA}{dt}=\frac{1}{2}r\times v`
`r\times v=\frac{J}{m}=constant`
Areal velocity,
`\frac{dA}{dt}=\frac{1}{2}\cdot\frac{J}{m}=constant`
It follows that the are velocity of the radius vector of planet relative to sun remains constant. This is Kepler's Second Law.
(iii) The Harmonic Law (Third Law)
This Law states that, "The square of the period of revolution of the planet around the sun is proportional to the cube of the semi-major axis of the ellipse."
`T^{2}∝a^{3}`
It is clear from the above equation that shorter the orbit of the planet around the sun, shorter the time taken to complete one revolution.
Dedication of Kepler's Third Law
Let T be period of revolution of the planet in elliptical orbit, area of ellipse = πab a and b being semi-major and semi-minor axes of the ellipse.
Areal velocity,
`\frac{dA}{dt}=\frac{J}{2m}`
∴ Period of revolution
`T=\frac{Area-of-ellipse}{Areal-velocity}`
`T=\frac{πab}{\frac{J}{2m}}`
`T^2=\frac{4π^{2}m^{2}a^{2}b^{2}}{J^2}`
If l is the semi-latus rectum of ellipse, then
`l=\frac{b^{2}}{a}`
`T^2=\frac{4π^{2}m^{2}a^{2}la}{J^2}`
i.e.,
`T^{2}∝a^{3}`
Since all other quantities are constant. This is Kepler's third law.