Motion in a Straight Line Class 11 notes Physics Chapter 3
▶Introduction
In the previous chapter, we have learnt about "Units and Measurement". In this chapter, we shall focus Motion in a Straight Line. Kinematics is the study of motion of physical bodies without going into the cause of its motion. In kinematics we deal with physical quantities like distance, displacement, speed, velocity and acceleration. Motion is common to everything in the universe. It is change in position of an object with time.
The earth rotates once every twenty-four hours and revolves round the sun once in a year. The sun itself is in motion in the Milky Way, which is again moving within its local group of galaxies. In this chapter, we shall study about Motion under Straight Line.
▶Rest and Motion
An object is said to be in motion with respect to an observer, if its position changes with time, with respect to that observer. Otherwise object is said to be in rest if their position does not change w.r.t. observer. Rest and motion are relative terms and are not absolute in nature.
▶Types of Motion
In order to completely describe the motion of an object, we need to specify its position. For this, we need to know the position co-ordinates. In some cases, three position co-ordinates are required, while in some cases two or one position co-ordinate is required. Based on these, motion can be classified as:
- One dimensional motion:- A particle moving along a straight-line or a path is said to undergo one dimensional motion. For example, motion of a train along a straight line, freely falling body under gravity etc.
- Two dimensional motion:- A particle moving in a plane is said to undergo two dimensional motion. For example, motion of a shell fired by a gun, carrom board coins etc.
- Three dimensional motion:- A particle moving in space is said to undergo three dimensional motion. For example, motion of a kite in sky, motion of aeroplane etc.
Read also: Motion In a Plane Class 11 Physics notes Chapter 4
▶Reference Frame
A frame with respect to which an observer observes the position and motion of an object is known as reference frame. For example if an observer observes the motion of an object while standing on earth then his frame of reference is earth. To describe the motion mathematically with respect to a frame of reference, a system of coordinates axis fixed on the reference frame is taken which are named as x, y and z-axis.
Recommended Books
- NCERT Textbook For Class 11 Physics Part 1 & 2
- CBSE All In One Physics Class 11 2022-23 Edition
- Oswaal CBSE Chapterwise Question Bank Class 11 Physics Book
- Modern's abc Plus of Physics for Class-11 (Part I & II)
Read also: Classification of Elements and Periodicity in Properties Class 11 Notes Chemistry Chapter 3
▶Point Object
If the length covered by the objects are very large in comparison to the size of the objects, the objects are considered as point objects.
▶Concept of Position, Distance and Displacement
▶Position
Position of a particle refers to its location in the space at a certain moment of time. In order to locate position of a particle with respect to a frame. We take three mutually perpendicular coordinate axes (x, y and z-axis) attached to this frame of reference.
▶Distance (Path Length)
We define distance as the actual path length traversed by a particle during its motion in a given interval of time. Distance is a scalar quantity as it has only magnitude and no direction. SI unit of measurement of distance is metre.
Read also: Conceptual Questions for Class 11 Physics Chapter 3 Motion in a Straight Line
▶Displacement
Displacement of a particle is the shortest distance between the initial and final position of the particle in a particular direction. It is a vector quantity and its SI unit of measurement is metre. The magnitude of displacement is always less than or equals to the total distance i.e.,
|Displacement| ≤ Distance
If a particle is moving along a straight line without changing the direction of motion then the distance and magnitude of displacement are equal.
▶Difference between Distance and Displacement
| S.No. | Distance | Displacement |
| 1. | Distance is a scalar quantity. | Displacement is a vector quantity. |
| 2. | Distance is the total path covered by the body. | Displacement is the shortest path covered by the body. |
| 3. | The distance can never be zero or negative. |
Displacement can be zero or negative. |
| 4. | Distance doesn’t decrease with time. | Displacement may be decrease. |
| 5. | Distance is always equal to or greater than the displacement. | Displacement is always equal to or less than the distance. |
▶Average Velocity and Average Speed
Average velocity is defined as the change in the position or displacement of a particle divided by the time interval in which the displacement occurs. The SI unit of velocity is m/s.
v = change in position / total time taken
`v=\frac{x_{2}-x_{1}}{t_{2}-t_{1}}`
Average speed, is defined as the total distance traveled divided by the total time interval during which the motion has taken place. The SI unit of speed is m/s.
average speed = Total-path-length / total-time-interval
▶Difference between Speed and Velocity
| S.No. | Speed | Velocity |
| 1. |
Speed is simply the rate of change of motion. | Velocity is the rate of change of position of an object with particular direction. |
| 2. |
Speed is the distance traveled by a body in a unit time. |
Velocity is the displacement covered by a body in a unit time. |
| 3. |
Speed is a scalar quantity. | Velocity is a vector quantity. |
| 4. |
Speed ascertains how fast a body moves. |
Velocity ascertains the object’s speed and the direction it takes while moving. |
| 5. |
Speed can never be zero. | velocity can be positive, negative or zero. |
▶Instantaneous Velocity and Instantaneous Speed
Instantaneous velocity gives the velocity of a particle at a particular instant of time. Thus the instantaneous velocity of a particle at a given instant of time is defined as the limit of average velocity as the time interval Δt, becomes infinitesimally small i.e.,
`v=\lim_{Δt \rightarrow 0}\frac{\text{Δ}x}{\text{Δ}t}`
and the limit of the ratio Δx/Δt as Δt approaches to zero is called the derivative of x w.r.t. t and is written as dx/dt .
Similarly instantaneous speed is the speed at a particular time.
▶Acceleration
The average acceleration a over a time interval is defined the change of velocity divided by the time interval in which that change occurred. The SI unit of acceleration is m/s2.
`v=\frac{v_{2}-v_{1}}{t_{2}-t_{1}}=\frac{\text{Δ}v}{\text{Δ}t}`
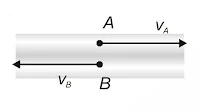
▶Relative Velocity
The velocity of one object w.r.t. other is known as relative velocity. So, we concluded that, if A and B are moving along the same direction then,
If A and B are moving in opposite directions then,
▶Equations of Motion
▶Derivation of velocity-time relation
By the definition of acceleration,
`a=\frac{\text{d}v}{\text{d}t}`
`\Rightarrow dv=adt`
Integrating both sides we get,
`\int dv=\int adt`
As acceleration is constant, therefore it comes out of integral.
Let at t = 0, initial velocity of particle is u and its final velocity at time t is v.
`\int_u^v dv=a\int_0^t dt`
v - u = at
v = u + at
▶Derivation of position-time relation
By the definition of velocity,
`v=\frac{\text{d}x}{\text{d}t}`
`\Rightarrow dx=vdt`
In the above equation, v is not independent of t. So we replace the value of v by v = u + at
dx = (u + at)dt
Let at t = 0, initial position of particle is 0 and its final position at time t is x from the chosen reference frame.
`\int_0^x dx=u\int_0^t dt+a\int_{0}^{t}tdt`
`x-0=ut+\frac{1}{2}at^2`
`s=ut+\frac{1}{2}at^2`
▶Derivation of velocity-displacement relation
Again we can write,
`a=\frac{dv}{dt}=\frac{dv}{dx}.\frac{dx}{dt}`
`a=v\frac{dv}{dx}`
v dv = a dx
`\int_{u}^{v}vdv= a\int_{0}^{x}dx`
`\frac{v^2-u^2}{2}=a(x-0)`
`v^2-u^2=2as`
where s = (x) is the displacement of the particle.
▶Displacement in nth second of uniformly accelerated motion
Let initial velocity of the object = uUniform acceleration of the object = a
Distance traveled by object in n second = sn
Distance traveled by object in (v – 1) second = sn – 1
Distance traveled by object in nth second = distance traveled by object in n second – distance traveled by object in (n – 1) second
▶Motion Under Gravity
A freely falling object is any object moving freely under the influence of gravity alone, regardless of its initial motion. Objects thrown upward or downward and those released from rest are all falling freely once they are released. Any freely falling object experiences an acceleration directed downward, regardless of its initial motion. We shall denote the magnitude of the free-fall acceleration by the symbol g.
v = u + gt
s = ut - 1/2g`t^2`
`v^2-u^2=-2gs`
▶Summary
An object is said to be in motion if its position changes and to specify the position of object, we need a reference point.
Path length or distance traversed by the object is always greater than or equal to the displacement of the object. When object is moving along a straight line, distance and displacement are equal.
In one dimensional motion of objects, the vector quantities like velocity, displacement, acceleration can have only two direction is +ve and –ve.
An object moving along a straight line is said to be in uniform motion, if it covers equal distance in equal intervals of time. Otherwise, its motion is non-uniform.
The average speed of an object is greater than or equal to the magnitude of the average velocity over a given time interval.
If a particle is speeding up acceleration is in the direction of velocity, and if the speed of the particle is decreasing, acceleration is in the direction opposite to that of the velocity.
The zero velocity of the object at any instant does not necessarily implies that its acceleration is zero. For example, an object thrown up has zero velocity at its upper most point but the acceleration at that instant is non-zero i.e. g, which is acceleration due to gravity.
For motion with uniform acceleration, x-t graph is a parabola while v-t graph is a straight line inclined to time-axis.
Slope of x-t graph of an object gives the velocity with which it is moving.
For uniform motion of an object acceleration is zero, x-t graph is a straight line inclineded to time-axis and v-t graph is a straight line parallel to time axis.
If x-t graph of an object is a straight line parallel to time axis, this implies that object is at rest.
The area under the velocity time graph gives the displacement of the object for a given time interval and the area under the acceleration-time graph gives the change in the velocity of the object under the given time interval.
Position-time graphs of two objects moving with same velocity are straight lines parallel to each other inclined to time axis.
If two objects are moving with unequal velocity, then the position graph of the object which is moving faster is steeper than the other and they meet at a common point.