Electrostatic Potential and Capacitance Class 12 Notes Physics Chapter 2
▶Introduction
In the previous chapter, we have learnt about "Electric Charges and Fields". In this chapter, we shall focus on Electrostatic Potential and Capacitance. The energy point of view can be used in electricity and it is especially useful. Energy is also a tool in solving Problems more easily in many cases than by using forces and electric fields.
Electric energy can be stored in a common device called a capacitor, which is found in nearly all electronic circuits. A capacitor is used as a storehouse for energy. Capacitors store the energy in common photo flash units.
▶Electrostatic Potential
The electrostatic potential (V) at any point in a region with the electrostatic field is the work done in bringing a unit positive charge (without acceleration) from infinity to that point. If 'W' is the work done in moving a charge ‘q’ from infinity to a point, then the potential at that point is V = W / q.
▶Electric Potential Difference
Similar to electric potential, the electric potential difference is the work done by external force in bringing a unit positive charge from point R to point P. i.e.,
`V_{P}-V_{R}=\frac{U_{P}-U_{R}}{q}`
Here VP and VR are the electrostatic potentials at P and R, respectively, and UP and UR are the potential energies of a charge q when it is at P and at R respectively.
Note: As before, it is not the actual value of potential but the potential difference that is physically significant. If, as before, we choose the potential to be zero at infinity, the above equation implies.
Read also: Current Electricity Class 12 Physics Notes Chapter 3
▶Unit for Electric Potential
The unit of measurement for electric potential is the volt, so the electric potential is often called voltage. A potential of 1 volt (V) equals 1 joule (J) of energy per 1 coulomb (C) of charge.
`1 V = 1 \frac{J}{C}`
▶Potential due to a Point Charge
Consider a point charge q placed at point O. Consider any point P in the field of the above charge. Let us calculate the potential at point P due to the charge q kept at a point O. Since the work done is independent of the path, we choose a convenient path, along the radial direction.
Let the distance OP = r.
The electric force at P, due to q will be directed along OP , given by
`F=\frac{1}{4\pi \epsilon_{o}}\frac{q q_{o}}{r^{2}}`
If the work done by moving this positive charge to dr distance is dW then,
dW = F (-dr)
`dW=-\int F.dr`
`dW=-\int_{∞}^{r} F.dr`
Hence, the total work done in bringing this charge from (∞) to 'r' will be,
`W=-\int_{∞}^{r} \frac{1}{4\pi \epsilon_{o}}\frac{q q_{o}}{r^{2}}.dr`
`W=-\frac{q q_{o}}{4\pi \epsilon_{o}}\int_{∞}^{r} \frac{1}{r^{2}}.dr`
`W=-\frac{q q_{o}}{4\pi \epsilon_{o}}\left[-\frac{1}{r}\right]_∞^r`
`W=\frac{1}{4\pi \epsilon_{o}}\frac{q q_{o}}{r^2}`
Hence, from V = W / qo, electric potential is,
`V=\frac{1}{4\pi \epsilon}_o \frac{q}{r}`
This equation is true for any sign of charge q. For q < 0, V < 0, i.e., work done by the external force per unit positive test charge to bring it from infinity to the point is negative. Also, this equation is consistent with the choice that the potential at infinity be zero.
Recommended Books
- NCERT Textbook For Class 12 Physics Part 1 & 2
- CBSE All In One Physics Class 12 2022-23 Edition
- Oswaal CBSE Chapterwise Question Bank Class 12 Physics Book
- Modern's abc Plus of Physics for Class-12 (Part I & II)
Read also: Solutions Class 12 Chemistry Notes Chapter 2
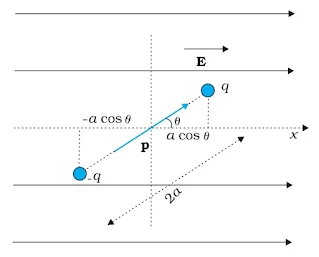
▶Potential due to an Electric Dipole
Consider dipole of length ‘2a’. Let P be a point at distance r1 from +q and r2 from -q. Let ‘r’ be the distance of P from the centre ‘O’ of the dipole. Let θ be an angle between dipole and line OP.
The potential due to +q,
`V_+=\frac{1}{4\pi \epsilon}_o \frac{+q}{r_1}`
The potential due to -q,
`V_- =\frac{1}{4\pi \epsilon}_o \frac{-q}{r_2}`
Therefore total potential,
`V=\frac{1}{4\pi \epsilon}_o \frac{+q}{r_1}\frac{1}{4\pi \epsilon}_o \frac{-q}{r_2}`
`V=\frac{q}{4\pi \epsilon}_o \left(\frac{1}{r_1}-\frac{1}{r_2}\right)`
`V=\frac{q}{4\pi \epsilon}_o \left(\frac{r_2-r_1}{r_1r_2}\right)`___(1)
From ∆ , we get (r2 – r1) = 2a cosθ
we can also take r2 = r1 = r (since ‘2a’ is very small) Substituting these values in equation (1), we get
`V=\frac{q}{4\pi \epsilon}_o \left(\frac{2a.cos\theta}{r^2}\right)`
`V=\frac{1}{4\pi \epsilon}_o \left(\frac{P.cos\theta}{r^2}\right)` (∵ P=2qa)
Case 1: If the point lies along the axial line of the dipole, then θ = 0°
`V=\frac{1}{4\pi \epsilon}_o \left(\frac{P.cos0}{r^2}\right)`
`V=\frac{1}{4\pi \epsilon}_o \left(\frac{P}{r^2}\right)`
Case 2: If the point lies along the equatorial line of the dipole, then θ = 90°
`V=\frac{1}{4\pi \epsilon}_o \left(\frac{P.cos90}{r^2}\right)`
V = 0
Read also: Conceptual Questions for Class 12 Physics Chapter 2 Electrostatic Potential and Capacitance
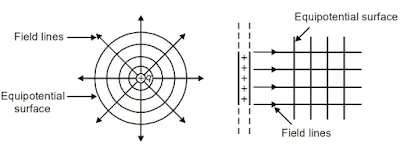
▶Equipotential Surfaces
An equipotential surface is a surface with a constant value of the potential at all points on the surface. For a single charge q, the potential is given by
`V=\frac{1}{4\pi \epsilon}_o \frac{q}{r}`
This shows that V is a constant if r is constant. Thus, equipotential surfaces of a single point charge are concentric spherical surfaces centered at the charge.
Example:- Note:- An equipotential surface is that at which, every point is at the same potential. As the work done is given by (VA – VB)q0
- Work done by electric field while a charge moves on an equipotential surface is zero as VA = VB
▶Relation between Electric Field and Potential Gradient
As we know that
`\triangle V=\frac{-W}{q_o}`
`V_f-V_i=\frac{-W}{q_o}` ___(1)
We know that,
`W=-\int F.dr` ___(2)
From eq. (1) and (2)
`V_f-V_i=\frac{-\int F.dr}{q_o}`
`V_f-V_i=\frac{-\int q_o E.dr}{q_o}`
`V_f-V_i=-\int E.dr`
The above result can also be expressed in differential form as,
`E=-\frac{dV}{dr}`
The negative sign in the expression signifies that as one moves in the direction of the electric field, potential decreases.
▶Potential Energy of a System of Charges
(i) Potential energy for a system of a two-point charge
The potential energy of a system of two charges is defined as the work done in assembling this system of charges at the given position from infinite separation.
Consider two charges q1 and q2 separated by distance r. Imagine q1 to be at A and q2 at infinity. The electric potential at B due to charge q1 is given by
`V=\frac{1}{4\pi\epsilon_o}\frac{q_1}{r}`
which is the work done in bringing unit positive charge from infinity to B. Therefore the work done in bringing charge q2 from infinity to B is
W = potential difference × charge
W = V × q2
`W=\frac{1}{4\pi\epsilon_o}\frac{q_1q_2}{r}`
This work done is stored as potential energy. Hence potential energy between the charges q1 and q2 is
`U=\frac{1}{4\pi\epsilon_o}\frac{q_1q_2}{r}`
(ii) Potential energy of a system of more than two charges
Let us find the potential energy of a system of three charges q1, q2 and q3 at positions r12 r23, and r31 respectively. The electric potential energy of this system is the sum of the potential of each pair. Hence we can write
`U=U_{12}+U_{23}+U_{31}`
`U=\frac{1}{4\pi\epsilon_o}\frac{q_1q_2}{r_{12}}+\frac{1}{4\pi\epsilon_o}\frac{q_2q_3}{r_{23}}+\frac{1}{4\pi\epsilon_o}\frac{q_3q_1}{r_{31}}`
`U=\frac{1}{4\pi\epsilon_o}\left(\frac{q_1q_2}{r_{12}}+\frac{q_2q_3}{r_{23}}+\frac{q_3q_1}{r_{31}}\right)`
(iii) Potential energy of a dipole in an external field
Consider a dipole of dipole moment ‘P’ suspended in a uniform electric field of intensity ‘E’. Let θ be the angle between P and E. Then we know torque τ = PE sinθ. Let the dipole be turned through an angle dθ then work done
dW = τdθ
dW = PE sinθ dθ
Total work done in rotating the dipole from θ1 to θ2
`W=\int_{\theta_1}^{\theta_2}PEsin\theta .d\theta`
W = PE (cosθ1 – cosθ2)
This work done is stored as potential energy.
▶Electrostatics of Conductors
Conductors contain mobile charge carriers. In metallic conductors, these charge carriers are electrons. In a metal, the outer (valence) electrons part away from their atoms and are free to move. These electrons are free within the metal but not free to leave the metal.
Whenever a conductor is placed in an external electric field, the free electrons in it experience a force due to it and start moving opposite to the field. This movement makes one side of the conductor positively charged and the other negatively charged. This creates an electric field in the conductor in a direction opposite to the external electric field (called induced field).
Important Points about Electrostatics of Conductors
(a) Inside a conductor, an electrostatic field is zero: In the previous chapter, we have already discussed that “when there is no electric current inside or on the surface of a conductor, the electric field inside the conductor is everywhere zero”.
(b) At the surface of a charged conductor, the electrostatic field must be normal to the surface at every point: If the field E is not normal to the surface, it will have a nonzero component along the surface. Hence the free charge on the surface will move due to electrostatic force on it. But free charge on the surface in electrostatics remains at rest. So the electrostatic field at the surface of a charged conductor must be normal to the surface.
(c) The interior of a conductor can have no excess charge in the static situation: In the previous chapter, we have already discussed it.
(d) Electrostatic Shielding: In an electrostatic situation, if a conductor contains a cavity and if no charge is present inside the cavity, then there can be no net charge anywhere on the surface of the cavity. This means that if you are inside a charged conducting box, you can safely touch any point on the inside walls of the box without being electrocuted. This is known as electrostatic shielding.
▶Dielectrics and Polarisation
Dielectrics are non-conducting substances. In contrast to conductors, they have no (or negligible number of) charge carriers. When a conductor is placed in an external electric field, the free charge carriers move and charge distribution in the conductor adjusts itself in such a way that the electric field due to induced charges opposes the external field within the conductor. This happens until, in the static situation, the two fields cancel each other and the net electrostatic field in the conductor is zero.
When a dielectric material is kept in an electric field, the external field induces a dipole moment by stretching or re-orienting molecules of the dielectric. This results in the development of net charges on the surface of the dielectric which produces a field that opposes the external field.
In general, the dielectric can be classified into Polar and Non-polar dielectrics. In a non-polar molecule, the centers of positive and negative charges coincide. The molecule thus has no permanent dipole moment. Examples of non-polar molecules are oxygen (O2) and hydrogen (H2) molecules which, because of their symmetry, have no dipole moment. On the other hand, a polar molecule is one in which the centers of positive and negative charges are separated (even when there is no external field). Such molecules have a permanent dipole moment. An ionic molecule such as HCl or a molecule of water (H2O) are examples of polar molecules.
The behavior of a non–polar dielectric:- In an external electric field, the positive and negative charges of a nonpolar molecule are displaced in opposite directions. The displacement stops when the external force on the constituent charges of the molecule is balanced by the restoring force. The non-polar molecule thus develops an induced dipole moment. The dielectric is said to be polarized by the external field.
The behavior of a polar dielectric:- A dielectric with polar molecules also develops a net dipole moment in an external field, but for a different reason. In the absence of an external field, the different permanent dipoles are oriented randomly due to thermal agitation; so the total dipole moment is zero. When an external field is applied, the individual dipole moments tend to align with the field.
▶Capacitors and Capacitance
A capacitor is a system of two conductors separated by an insulator. If two conductors have a potential difference between them then, as any potential difference is able to accelerate charges, the system effectively stores energy. Such a device that can maintain a potential difference, storing energy by storing charge is called a capacitor. When charges +Q and –Q are given to two plates, a potential difference is developed between the plates. The capacitance of the arrangement is defined as C = Q / V
Definition of Capacitance:- Capacitance is defined as the amount of charge required to raise the potential of a conductor by one volt.
The capacity of an isolated spherical conductor
Consider a sphere with center O and radius r, which is supplied with a charge = +q. This charge is distributed uniformly over the outer surface of the sphere. Thus, the potential at every point on the surface is the same and is given by
`V=\frac{q}{4\pi\epsilon_0 r}`
As, C = Q / V
`C=4\pi\epsilon_0 r`
▶The Parallel Plate Capacitor
The arrangement consists of two thin conducting plates, each of area A and separated by a small distance d. When charge q is given to the first plate, a charge –q is induced on the inner face of the other plate and positive on the outer face of the plate. As this face is connected to the earth, a net negative charge is left on this plate. Thus, the arrangement is equivalent to two thin sheets of charge. As d is much smaller than the linear dimension of the plates (d2 << A), we can use the result of the electric field by an infinite sheet of charge. The electric field between the plates is
`E=\frac{\sigma}{2\epsilon_0}+\frac{\sigma}{2\epsilon_0}`
`E=\frac{\sigma}{\epsilon_0}`......(1)
For uniform field potential difference between the plates.
`V=Ed=\frac{\sigma d}{\epsilon_0}`.....from eq(1)
`V=\frac{qd}{\epsilon_0 A}` as σ = q / A
`C=\frac{q}{V}=\frac{q}{\frac{qd}{\epsilon_0 A}}`
`C=\frac{\epsilon_0 A}{d}`
▶Effect of Dielectric on Capacitance
When a dielectric slab of dielectric constant K is inserted between the plates filling the entire space between the plates. The plates of the capacitor are given charge +Q and –Q and hence induced charges –QP and +QP appear on the surfaces of the slab. So, capacitance is increased to K times when the space between the plates is filled with a dielectric of dielectric constant K.
▶Combination of Capacitors
(i) Series Grouping
The arrangements shown in the figure are examples of series grouping. When capacitors can be arranged in a row, so that there is no connection between two capacitors to any third capacitor, it is called a series combination. Or, when the same charge flows through each capacitor connected.
`\frac{1}{C}=\frac{1}{C_1}+\frac{1}{C_2}+\frac{1}{C_3}`
(ii) Parallel Grouping
The arrangements shown in the figure are examples of parallel combinations. When two or more capacitors are connected between two given points, they are said to be in parallel. Or, when the capacitor bears the same potential difference across it.
`C=C_1+C_2+C_3`
▶Energy Stored in a Capacitor
During the charging of a capacitor, work has to be done to add a charge to the capacitor against its potential. This work is stored in the capacitor as electrical energy. Suppose during the charging of the capacitor its potential at any instant is given by
`V=\frac{q}{C}`
A small amount of work done in adding a charge dq is given by
`dw=\frac{q}{C}dq`
Total work done in giving a charge Q to the condenser is
`w=\int_{0}^{Q}\frac{q}{C}dq`
`w=[\frac{q^2}{2C}]_0^Q`
`w=\frac{Q^2}{2C}`
`U=\frac{Q^2}{2C}=\frac{1}{2}CV^2=\frac{1}{2}QV`
▶Van de Graaff Generator
Van de Graaff generator is a machine that can build up voltages in the order of a few million volts. The resultant electric fields are used to accelerate charged particles (protons, electrons, ions) to the high energies required for experiments to examine the small-scale structure of matter.
If you want more details on the Van de Graaff generator you may click here.
▶Summary
Electrostatic potential (V) is the scalar way of representing the region around a charge configuration which is useful in calculating the work involved when a charge moves around other charges or in a field.
Potential is a scalar quantity and it may be positive, negative, or zero.
S.I. unit of potential is volt or joule per coulomb.
Equipotential surfaces never intersect each other.
If we go away from a positive charge, potential decreases but if we go away from a negative charge, potential increases.
If we move in the direction of the electric field then the potential decreases.
The capacitor is basically an energy storage device. We keep multiple plates in it so that large energy can be stored in it without increasing the size of a capacitor.
Capacitors are combined in parallel when we require a big amount of charge at a small potential.
The capacitance of the earth is approximately 711 μF.
S.I. unit of capacitance is coulomb/volt or farad (F) in honour of Michael Faraday.
When a dielectric material is placed in an electric field the phenomenon of reorientation of polar molecules or the shifting of the positive and negative charge distributions in an atom or a nonpolar molecule of the material is called the polarization of the atom or molecule.
If a capacitor is charged by a battery of potential V, then work done by the battery is double the energy stored in the capacitor. The extra energy is lost as heat and electromagnetic radiation due to the transient current during the charging process.
In 1929, Rober J. Van de Graaff designed a machine that could build up high voltages of the order of a few million volts. This machine acts on the principle of corona discharge.