Electric Charges and Fields Class 12 Notes Physics Chapter 1
▶Introduction
The study of static charges is called electrostatics and this complete electrostatic will be discussed in two chapters. In this chapter, we begin with a discussion of electric charge, some properties of charged bodies, and the fundamental electric force between two charged bodies.
▶What is Electric Charge?
Electric Charge is a fundamental property of a matter which is responsible for electric forces between the bodies. Two electrons placed at a small separation are found to repeal each other, this repulsive force (Electric force) is only because of the electric charge on electrons.
When a glass rod is rubbed with silk, the rod acquires one kind of charge and the silk acquires the second kind of charge. This is true for any pair of objects that are rubbed to be electrified. Now if the electrified glass rod is brought in contact with silk, with which it was rubbed, they no longer attract each other.
Types of Electric Charge
There are two types of charges that exist in our nature.
- Positive Charge
- Negative Charge
If any object loses its electrons then they get a positive charge. It is denoted by (+q) sign. If any object gain electrons from another object then it gets a negative charge. It is denoted by (-q) sign. The charges were named as positive and negative by the American scientist Benjamin Franklin. If an object possesses an electric charge, it is said to be electrified or charged. When it has no charge it is said to be neutral.
Read also: Electrostatic Potential and Capacitance Class 12 Physics Notes Chapter 2
▶Basic Properties of Electric Charge
The important properties and characteristics of electric charge are given below.
(i) Attraction and Repulsion:- Like charges repel each other while unlike charges attract each other.
(ii) Electric Induction:- When a charged object brings to contact with another uncharged, it gets the opposite charge of the charged object. It is called charging by induction.
(iii) Charge is Quantized:- An object that is electrically charged has an excess or deficiency of some whole number of electrons. Since electrons cannot be divided into fractions of electrons, it means that the charge of an object is a whole-number multiple of the charge of an electron. For example, it cannot have a charge equal to the charge of 0.5 or 1000.5 electrons.
Mathematically q = ± ne, Here n = 1, 2, 3 and e = 1.6 × 10–19 coulomb.
(iv) Electric Charge is Conserved:- According to this property, "An electric charge neither can be created nor can be destroyed" i.e. total net charge of an isolated system is always conserved. Thus, when a glass rod is rubbed with silk cloth, both glass rod, and silk cloth acquire opposite charges in the same quantity. Thus, the total amount of charge remains the same before rubbing as well as after rubbing.
Recommended Books
- NCERT Textbook For Class 12 Physics Part 1 & 2
- CBSE All In One Physics Class 12 2022-23 Edition
- Oswaal CBSE Chapterwise Question Bank Class 12 Physics Book
- Modern's abc Plus of Physics for Class-12 (Part I & II)
Read also: Solid State Class 12 Chemistry Notes Chapter 1
▶Conductors and Insulators
Some substances easily allow the passage of electricity through them while others do not. Substances that allow electricity to pass through them easily are called ‘conductors’. They have electrons that are free to move inside the material. Metals, human and animal bodies, earth, etc. are examples of conductors. Non-metals e.g., glass, plastic, and wood are ‘insulators’ because they do not easily allow the passage of electricity through them.
Most substances are either conductors or insulators. There is a third category called ‘semiconductors’ which are intermediate between conductors and insulators because they partially allow movement of charges through them.
▶Charging by Induction
Now as we know that two oppositely charged bodies attract each other. But it also has been our observation that a charged body attracts a neutral body as well. This is explained on the basis of charging by induction. In the induction process, two bodies (at least one body must be charged) are brought very close, but they never touch each other.
 |
| Charging by Induction |
Read also: Conceptual Questions for Class 12 Physics Chapter 1 Electric Charges and Fields
Let us examine how a charged body attracts an uncharged body. Imagine a conducting or partially conducting body (sphere here) is kept on an insulating stand and a charged rod (positive, for example) is brought very close to it. It will attract electrons to its side and the farther end of the sphere will become positively charged as it is deficient in electrons.
▶Coulomb’s Law
In 1785 Charles Coulomb (1736-1806) experimentally established the fundamental law of electric force between two stationary charged particles. He observed that An electric force between two charged particles has the following properties:
- It is directed along a line joining the two particles and is inversely proportional to the square of the separation distance r, between them.
- It is proportional to the product of the magnitudes of the charges, |q1| and |q2|, of the two particles.
- It is attractive if the charges are of opposite sign and repulsive if the charges have the same sign.
From these observations, Coulomb proposed the following mathematical form for the electric force between two charges. The magnitude of the electric force F between charges q1 and q2 separated by a distance r is given by
`F=k\frac{|q_{1}||q_{1}|}{r^{2}}`
where k is a constant called the Coulomb constant. The proportionality constant k in Coulomb’s law is similar to G in Newton’s law of gravitation. Instead of being a very small number like G (6.67 × 10–11), the electrical proportionality constant k is a very large number. It is approximately
k = 8.9875 × 109 N-m2C–2
The constant k is often written in terms of another constant, ε0, called the permittivity of free space. It is related to k by
`k=\frac{1}{4\pi \epsilon_o}`
`\therefore F=\frac{1}{4\pi \epsilon_o}\frac{|q_{1}||q_{1}|}{r^{2}}`
`\epsilon_o=\frac{1}{4\pi k}=8.85\times 10^{-12}` C2 / Nm2
▶Electric Field
A charge produces something called an electric field in the space around it and this electric field exerts a force on any charge (except the source charge itself) placed in it. The electric field has its own existence and is present even if there is no additional charge to experience the force.
▶Intensity of Electric Field
The intensity of the electric field due to a charge configuration at a point is defined as the force acting on a unit positive charge at this point. Hence if a charge q experiences an electric force F at a point then the intensity of the electric field at this point is given as
E = F / q
It has S.I. units of newtons per coulomb (N/C).
▶Electric Field due to a Point Charge
To determine the direction of an electric field, consider a point charge q as a source charge. This charge creates an electric field at all points in the space surrounding it. A test charge q0 is placed at point P, a distance r from the source charge. According to Coulomb’s law, the force exerted by q on the test charge is
`F=\frac{1}{4πε_0}\frac{qq_0}{r^2}`
This force is directed away from the source charge q, since the electric field at P, the position of the test charge, is defined by
`E=\frac{F}{q_0}`
we find that at P, the electric field created by q is
`E=\frac{1}{4πε_0}\frac{q}{r^2}`
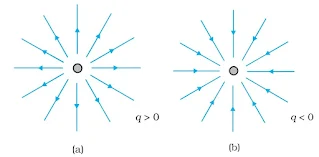
▶Electric Field Lines
Electric field lines are a way of pictorially mapping the electric field around a configuration of charges. An electric field line is, in general, a curve drawn in such a way that the tangent to it at each point is in the direction of the net field at that point. The field lines follow some important general properties:
- The tangent to electric field lines at any point gives the direction of the electric field at that point.
- In free space, they are continuous curves that emerge from a positive charge and terminate at a negative charge
- They do not intersect each other. If they do so, then it would mean two directions of the electric field at the point of intersection, which is not possible.
- Electrostatic field lines do not form any closed loops. This follows from the conservative nature of the electric field
▶Electric Dipole
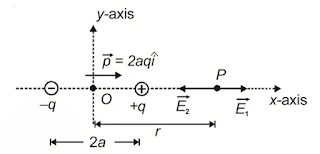
A configuration of two charges of the same magnitude q, but of opposite sign, separated by a small distance (say 2a) is called an electric dipole.
The dipole moment for an electric dipole is a vector quantity directed from the negative charge to the positive charge and its magnitude is p = q × 2a (charge × separation). The SI unit of dipole moment is C-m (coulomb-metre).
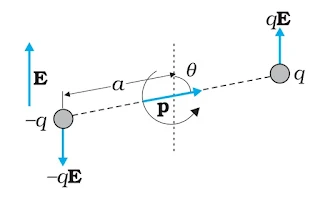 |
| Electric Dipole |
▶Electric Field Strangth due to Electric Dipole
▶(i) At Axial Position
The net electric field at P
`E=\vec{E_1}+\vec{E_2}`, where E1 and E2 are fields due to +q and –q respectively
`E_1=\frac{1}{4\pi\epsilon_0}\frac{q}{(r-a)^2}` .....(1)
`E_2=\frac{1}{4\pi\epsilon_0}\frac{-q}{(r+a)^2}` .....(2)
`E=E_{1}+E_{2}`
From eq. (1) and (2)
`E=\frac{q}{4\pi\epsilon_0}[\frac{1}{(r-a)^2}-\frac{1}{(r+a)^2}]`
`E=\frac{q}{4\pi\epsilon_0}[\frac{(r+a)^2-(r-a)^2}{(r^{2}-a^{2})^2}]`
`E=\frac{q}{4\pi\epsilon_0}\frac{4ar}{(r^{2}-a^{2})^2}`
`E=\frac{1}{4\pi\epsilon_0}\frac{2(2aq)r}{(r^{2}-a^{2})^2}`
`E=\frac{1}{4\pi\epsilon_0}\frac{2Pr}{(r^{2}-a^{2})^2}`
For a short dipole, a is very small in comparison
`\therefore r^{2}-a^{2}\approx r^2`
`E=\frac{1}{4\pi\epsilon_0}\frac{2P}{r^3}`
▶(ii) At Broad side on Position
Electric field vector due to +q is
`E_1=\frac{1}{4\pi\epsilon_0}\frac{q}{(r^{2}+a^2)}`
Electric field vector due to –q is
`E_2=\frac{1}{4\pi\epsilon_0}\frac{q}{(r^{2}+a^2)}`
Resultant field at P is,
`E=E_{1}cos\theta+E_{2}cos\theta`
`E=\frac{1}{4\pi\epsilon_0}\frac{q}{(r^{2}+a^2)}cos\theta+\frac{1}{4\pi\epsilon_0}\frac{q}{(r^{2}+a^2)}cos\theta`
`E=\frac{1}{4\pi\epsilon_0}\frac{2q}{(r^{2}+a^2)}cos\theta`
`E=\frac{1}{4\pi\epsilon_0}\frac{2q}{(r^{2}+a^2)}\frac{a}{\sqrt{r^{2}+a^2}}`
`E=\frac{1}{4\pi\epsilon_0}\frac{2aq}{(r^{2}+a^2)^{\frac{2}{3}}}`
`E=\frac{1}{4\pi\epsilon_0}\frac{P}{(r^{2}+a^2)^{\frac{2}{3}}}`
For a short dipole
`\therefore r^{2}+a^{2}\approxr^2`
`E=\frac{1}{4\pi\epsilon_0}\frac{P}{(r^{2}+a^2)^3}`
▶Torque of Electric Dipole in uniform Electric Field
An electric dipole is placed in a uniform electric field E
The force experienced by the dipole is
F = qE
The two forces form a couple and it tries to turn the dipole. The torque due to the couple is given by
τ = either force × perpendicular distance between the forces
τ = qE × (2a sin θ)
τ = (2aq) E sin θ
τ = pE sin θ
τ = p × E
▶Electric Flux
The number of electric field lines that are passing perpendicular through the unit surface of any plane is called electric flux. Consider an electric field that is uniform in both magnitude and direction, as in the figure.
We can write this as N ∝ EA, which means that the number of field lines is proportional to the product of E and A. This is a measure of electric flux and is represented by the symbol φ. In the above case, φ = EA cosθ. The SI unit of electric flux is N-m2/C or V-m(volt-metre).
▶Solid Angle
A solid angle is defined as an angle that is made at a point in place by an area. The SI unit of solid angle is steradian, and it is expressed as 'sr'.
`sr=\frac{dA\cos\theta}{r^2}`
▶Gauss’s Law
It states that the electric flux Φ through any closed surface is equal to (1/εo) times the net charged q enclosed by the surface. That is
`\phi =\int E.dS=\frac{q}{\epsilon_o}`
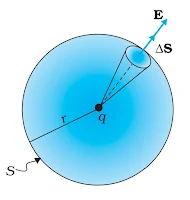
Proof: Consider a point charge q surrounded by a spherical surface of radius r centered on the charge. The magnitude of the electric field everywhere on the surface of the sphere is
`E=\frac{1}{4πε_0}\frac{q}{r^2}` ......(1)
The electric field is perpendicular to the spherical surface at all points on the surface. The electric flux through the surface is
`\phi_{E}=\int EA\cos\theta` .....(2)
Putting the value of E from eq. (1)
`\phi_{E}=\int \frac{1}{4πε_0}\frac{q}{r^2}A\cos\theta`
`\phi_{E}=\frac{q}{4πε_0}\int \frac{A\cos\theta}{r^2}`
`\phi_{E}=\frac{q}{4πε_0}\int d\omega`
`\phi_{E}=\frac{q}{4πε_0} 4\pi`
`\phi_{E}=\frac{q}{ε_0}`
This result says that the electric flux through a sphere that surrounds a charge q is equal to the charge divided by the constant ε0
Let us note some important points regarding this law:
- Gauss’s law is true for any closed surface, no matter what its shape or size.
- The term q on the right side of Gauss’s law, includes the sum of all charges enclosed by the surface.
- Gauss’s law is often useful for a much easier calculation of the electrostatic field when the system has some symmetry.
- Gauss’s law is based on the inverse square dependence on distance contained in Coulomb’s law.
▶Application of Gauss’s Law
- It is used to calculate electric field due to an infinitely long straight uniformly charged wire.
- It is also used to calculate electric field due to a uniformly charged infinite plane sheet.
- It is also used to calculate electric field due to a uniformly charged thin spherical shell.
(i). Electric field strength due to an infinitely long straight uniformly charged wire
Let a charged wire of infinite length be +q charge and its linear charge density λ be. To calculate the electric field due to this wire, let us assume a cylindrical Gaussian surface of radius r. Let the area of this Gaussian surface be dS1, dS2, dS3.
Hence the total electric flux passing through the first surface dS1,
`\phi_{1}=\oint E.dS_1 cosθ`
`\phi_{1}=\oint E.dS_1 cos90°`
`\phi_1=0` .....(1)
Similarly, the total electric flux passing through the second surface dS2,
`\phi_{2}=\oint E.dS_2 cosθ`
`\phi_{2}=\oint E.dS_2 cos0`
`\phi_{2}=\oint E.dS_2`
`\phi_{2}=E\oint dS_2`
`\phi_{2}=E(2\pi rl)` .....(2)
Similarly, the total electric flux passing through the third surface dS3,
`\phi_{3}=\oint E.dS_3 cos90°`
`\phi_3=0` .....(3)
Hence, the total electric flux passing through the Gaussian surface,
`\phi=\phi_1+\phi_2+\phi_3`
`\phi=0+E.2\pi rl+0`
`\phi=E.2\pi rl` .....(4)
Putting `\phi= \frac{q}{\epsilon_0}` from Gauss's theorem,
`\frac{q}{\epsilon_0}=E.2\pi rl`
`E=\frac{\frac{q}{l}}{2\pi r\epsilon_0}`
`E=\frac{\lambda}{2\pi r\epsilon_0}`
▶Deduction of Coulomb’s law from Gauss' Law
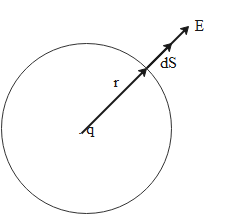
Consider a charge +q in place at origin in a vacuum. We want to calculate the electric field due to this charge at a distance r from the charge. Imagine that the charge is surrounded by an imaginary sphere of radius r as shown in the figure below. This sphere is called the Gaussian sphere.
Consider a small area element dS on the Gaussian sphere. We can calculate the flux through this area element due to charge as follows:
`\oint \vec{E}.\vec{dS}=E\int dS`
`\oint \vec{E}.\vec{dS}=E(4\pi r^2)`
Using this in Gauss theorem we get
`E(4\pi r^2)=\frac{q}{\epsilon_0}`
`E=\frac{1}{4\pi\epsilon_0}\frac{q}{r^2}`
We know that
`F=Eq_0`
`F=\frac{1}{4\pi\epsilon_0}\frac{qq_0}{r^2}`
This is the required Coulomb’s law obtained from the Gauss theorem.
▶Summary
A charge is a property associated with the matter due to which it produces and experiences electrical and magnetic effects.
The force between two point charges at rest varies directly as the product of the magnitude of each charge and inversely as the square of the distance between them.
The force experienced by a unit positive point charge is called electric field intensity.
A field line is an imaginary curve, such that the tangent to which at a point gives the direction of the electric field at that point.
If two equal and opposite point charges q are separated by a distance of 2a, then the electric dipole moment is defined as a vector quantity having magnitude p = q × 2a and direction from negative to positive charge.
The electric flux through an elementary area vector ds is defined as the dot product of electric field intensity E and ds.
The total electric flux linked with a closed surface is (1/εo) times the net charge enclosed by the closed surface.