Semiconductor Material | n-type and p-type Semiconductor
Types of Material
On the basis of the relative values of electrical conductivity (σ) or resistivity (ρ), we can classify the solid materials in following three broad categories.
1. Conductors
The substances by which charge is flowed in free are called conductors. The conductivity of these conductors is by free electrons and resistivity is of the order of 10-8 to 10-6 Ωm. As:- Silver, Copper, Aluminium etc.
2. Insulators
The substances by which charge is never flowed are called Insulators. The resistivity of these insulators is of the order of 1011 to 1019 Ωm. As:- Wood, Polythene, Plastic etc.
3. Semiconductors
Semiconductors are the materials having resistivity or electrical conductivity intermediate to Conductors and insulators. At absolute zero temperature, a semiconductor is an ideal insulator. However, at room temperatures of about 300 K, their resistivity ranges from 10-5 to 106 Ωm and their electrical conductivity varies from 105 to 10-6 Ωm. These have few conduction electrons and holes for conduction.
Types of Semiconductors
On the basis of the doping, Semiconductors can be classified in two types.
(i) Intrinsic Semiconductor
Pure semiconductors are called intrinsic semiconductors. In an intrinsic semiconductor, the presence of charge carriers in an intrinsic property of the material and these are obtained as result of thermal excitation. Silicon and Germanium are two examples of intrinsic semiconductors. The electrical conductivity of an intrinsic semiconductor cannot be controlled because it depends on its temperature. Moreover, at room temperature, the magnitude of the conductivity is very low and as such no important electric device can be developed using intrinsic semiconductors. In an intrinsic semiconductor, free electrons are equal to holes. i.e.
ne = nh
Crystal lattice of pure Silicon Semiconductor |
(ii) Extrinsic Semiconductor
Semiconductors with suitable impurity added to them in a controlled quantity are known as, extrinsic semiconductors and extrinsic semiconductor is also called an impurity semiconductor or Doped semiconductor. The process of deliberate addition of a desirable impurity in a controlled quantity to a pure semiconductor is called 'doping' and the impurity atoms are called the dopants. This can be further divided into following two types :
(a) p-type Semiconductor
A p-type semiconductor is obtained when silicon is doped with a trivalent impurity like Al, B, Ga, In etc. As the dopant atom has 1 valence electron less than Silicon, the atom can form only three covalent bonds with three neighbouring Si atoms but does not have any electron to offer to the fourth neighbouring Silicon atom. Thus, the bond between fourth Si neighbour and the Al atom has a vacancy or hole as shown in figure.
 |
| Crystal lattice of p-type Semiconductor |
Since the neighbouring Silicon atoms in lattice wants an electron, in place of hole, an electron from the outer orbit of neighbouring atoms may jump to fill this vacancy living a hole at its own site. Thus, a hole is available for conduction. Due to this, extrinsic semiconductors doped with trivalent impurity are called p-type semiconductor. For a p-type semiconductor, ne<<nh.
(b) n-type semiconductor
A n-type semiconductor is obtained when a pentavalent atom occupies the position of the Silicon atoms in the crystal lattice of silicon, 4 of its Valence Electrons form covalent bonds with the four Silicon neighbours but fifth Valence Electrons remains very weekly Bound to its parent atom. Consequently, the ionization energy required to set this electrons free is very small. This fifth electron of dopant atom is free to move in the lattice of the semiconductor and effectively, it means that the each pentavalent dopant atoms is donating and extra electrons for conduction. Therefore, these semiconductors are known as n-type semiconductors. For n-type semiconductor, ne>>nh
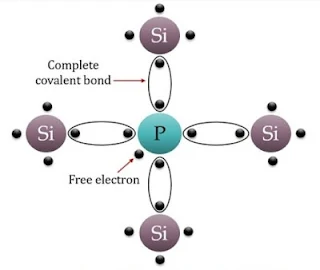 |
| Crystal lattice of n-type Semiconductor |
The electron and hole concentration in a extrinsic semiconductor in thermal equilibrium is given by the relation :
`n_e.n_h=n_i^2`
Where, ni = number density of intrinsic charge-carriers in the pure semiconductor.

