Ray Optics and Optical Instruments Class 12 notes Physics Chapter 9
Introduction
In the present chapter, we shall study the phenomena like reflection, refraction, and dispersion of light. We then go on to describe the construction and working of some important optical instruments, including the human eye.
We can see objects because of the light reflected or emitted by them. Nature has given us eyes, which can detect a small region of the electromagnetic radiation spectrum. This region (visible to us) is called light. From common experience, we can say that light travels with a great speed and that it travels in a straight line.
Reflection of Light
The phenomenon in which a light ray is sent back into the same medium from which it is coming, on interaction with a boundary, is called reflection. The boundary can be a rigid surface or just an interface between two media.
Law of reflection
The angle of reflection equals the angle of incidence ∠i = ∠r.
The incident ray reflected ray and the normal to the reflecting surface at the point of incidence lie in the same plane.
Spherical Mirrors
A spherical mirror is a part of a sphere. If one of the surfaces is silvered, the other surface acts as the reflecting surface. When the convex face is silvered, and the reflecting surface is concave, the mirror is called a concave mirror. When its concave face is silvered and a convex face is a reflecting face, the mirror is called a convex mirror.
Centre of curvature: Centre of curvature is the center of a sphere of which, the mirror is a part.
The radius of curvature: The radius of curvature is the radius of the sphere of which, the mirror is a part.
Pole of the mirror: Pole is the geometric center of the mirror.
Principal axis: Principal axis is the line passing through the pole and center of curvature.
Normal: Any line joining the mirror to its center of curvature is normal.
Recommended Books
- NCERT Textbook For Class 12 Physics Part 1 & 2
- CBSE All In One Physics Class 12 2022-23 Edition
- Oswaal CBSE Chapterwise Question Bank Class 12 Physics Book
- Modern's abc Plus of Physics for Class-12 (Part I & II)
Read also: Wave Optics Class 12 Physics Notes Chapter 10
Sign Convention
According to the Cartesian sign convention, all distances are measured from the pole of the mirror or the optical center of the lens.
The distances measured in the same direction as the incident light are taken as positive and those measured in the direction opposite to the direction of incident light are taken as negative.
The heights measured upwards with respect to the x-axis and normal to the principal axis of the mirror/lens are taken as positive. The heights measured downwards are taken as negative.
According to this, the focal length of a convex mirror/lens is the positive and the focal length of a concave mirror/lens is negative.
Focal Length of Spherical Mirrors
When a parallel beam of light is incident on a concave mirror, and a convex mirror. The rays are incident at points close to the pole P of the mirror and make small angles with the principal axis. The reflected rays converge at a point F on the principal axis of a concave mirror. For a convex mirror, the reflected rays appear to diverge from a point F on its principal axis.
Point F is called the principal focus of the mirror. The distance between the focus F and the pole P of the mirror is called the focal length of the mirror, denoted by f.
If R be the radius of curvature of the mirror then the relation between R and f is given by
`f=\frac{R}{2}`
Read also: Coordination Compounds Chemistry Class 12 Notes Chapter 9
Number of images formed by two plane mirrors
Consider two plane mirrors inclined at an angle θ (in degrees) with each other. Multiple reflections take place from the surfaces of these mirrors and more than one image is formed. To find out a number of images, we compute `n=[\frac{360°}{\theta}]`. Now, if
n is even, number of images = n – 1
n is odd, the number of images equals
Refraction
When light travels from one transparent medium to another, it deviates from its original path. The phenomenon of change in the path of light at the medium of separation as it goes from one medium to another medium is called refraction.
Snell’s Law
The incident ray, the refracted ray, and the normal to the interface at the point of incidence, all lie in the same plane.
Normal at the medium of separation and ‘i’ and ‘r’ are the angles of incidence and refraction respectively then for pair of media and for a given color `\frac{sin i}{sin r}=\mu_{21}`= Constant
`\mu_{21}` is called the refractive index of the second medium w.r.t. first medium.
Absolute Refractive index
The absolute refractive index of a medium is defined by the ratio of the speed of light in a vacuum to the speed of light in the medium `\mu=\frac{c}{v}`, where c is the speed of light in a vacuum and v is the speed of light in the medium.
Read also: Conceptual Questions for Class 12 Physics Chapter 9 Ray Optics and Optical Instruments
Total Internal Reflection
When light travels from an optically denser medium to a rarer medium at the interface, it is partly reflected back into the same medium and partly refracted to the second medium. This reflection is called internal reflection.
When a ray of light enters from a denser medium to a rarer medium, it bends away from the normal, the angle of refraction (r) being larger than the angle of incidence (i). As the angle of incidence increases, so does the angle of refraction, till, for the ray, the angle of refraction is 90º. The angle of incidence corresponding to an angle of refraction 90º is called the critical angle (ic). If the angle of incidence is increased still further, refraction is not possible, and the incident ray is totally reflected. This is called total internal reflection.
`sin i_{c}=\frac{\mu_1}{\mu_2}`
Application of Total Internal Reflection
(i). Mirage
On hot summer days, the air near the ground becomes hotter than the air at higher levels. The refractive index of air increases with its density. Hotter air is less dense and has a smaller refractive index than cooler air. If the air currents are small, that is, the air is still, and the optical density at different layers of air increases with height.
As a result, light from a tall object such as a tree passes through a medium whose refractive index decreases towards the ground. Thus, a ray of light from such an object successively bends away from the normal and undergoes total internal reflection, if the angle of incidence for the air near the ground exceeds the critical angle. To a distant observer, the light appears to be coming from somewhere below the ground.
The observer naturally assumes that light is being reflected from the ground, say, by a pool of water near the tall object. Such inverted images of distant tall objects cause an optical illusion to the observer. This phenomenon is called mirage. This type of mirage is especially common in hot deserts.
(ii). Diamond
The critical angle for the diamond-air interface (≈ 24.4°) is very small, therefore once light enters in diamond, it undergoes total internal reflections inside it, as a result, it sparkles brilliantly. By cutting the diamond suitable multiple total internal reflections can be made to occur.
(iii) .Prism
Prisms are designed to bend light by 90° or 180° the phenomenon of total internal reflection, such prisms are used to invert images without changing their size.
(iv). Optical fibres
Optical fiber is a transmission medium to carry the optical signal without any appreciable loss. The structure of optical fiber consists of a core surrounded by cladding. The core is the denser medium of refractive index μ1 and cladding is the relatively rarer medium of refractive index μ2 such that μ1 > μ2.
When a light incident at one end of the core gets refracted and will be incident on the interface between the core and cladding at an angle greater than the critical angle and the light continues reflecting in the core.
Lens Formula
The lens formula relates the distance of the object from the lens with the distance of the image from the lens. It is given by
`\frac{1}{f}=\frac{1}{v}-\frac{1}{u}`
Where u = object distance
v = image distance
f = focal length
Mirror Formula
The mirror formula relates the distance of the object from the mirror with the distance of the image from the mirror. It is given by
`\frac{1}{f}=\frac{1}{v}+\frac{1}{u}`
Where u = object distance
v = image distance
f = focal length
Lens Maker’s Formula
Lens Maker’s formula gives the focal length of a lens in terms of the nature of the surfaces by which the lens is bounded and the nature of the material of the lens.
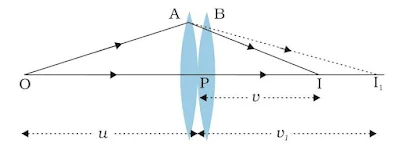
Let us consider the situation shown in the figure. C1 and C2 are the centers of curvature of two spherical surfaces of the thin lens. O is the object and I' is the image due to the first refraction. Let radii of curvature be R1 and R2.
For the first refraction at image distance is v1. From the formula for refraction at a curved surface, we get
`\frac{n_2}{v_1}-\frac{n_1}{u}=\frac{n_{2}-n_{1}}{R_1}` .....(i)
Final image position is I, which is also the image due to second refraction. Let this image distance be v. For the second refraction, v1 becomes the object distance. Hence we get,
`\frac{n_1}{v}-\frac{n_2}{v_1}=\frac{n_{1}-n_{2}}{R_2}` .....(ii)
Adding (i) and (ii), we get
`(\frac{n_{1}}{v}-\frac{n_{1}}{u})=(n_{2}-n_1)(\frac{1}{R_1}-\frac{1}{R_2})`
`\frac{1}{v}-\frac{1}{u}=(\frac{n_2}{n_1}-1)(\frac{1}{R_1}-\frac{1}{R_2})`
`\frac{1}{v}-\frac{1}{u}=(n-1)(\frac{1}{R_1}-\frac{1}{R_2})`
According to the definition of the focal length f
`\frac{1}{f}=(n-1)(\frac{1}{R_1}-\frac{1}{R_2})`
This is called the “Lens Maker’s formula”.
Combination of thin lenses in contact
Consider two lenses A and B of focal length f1 and f2 placed in contact with each other. Let the object be placed at a point O beyond the focus of the first lens A. The first lens produces an image at I1. Since image I1 is real, it serves as a virtual object for the second lens B, producing the final image at I.
For the image formed by the first lens A, we get
`\frac{1}{v_1}-\frac{1}{u}=\frac{1}{f_1}` .....(i)
For the image formed by the second lens B, we get
`\frac{1}{v}-\frac{1}{v_1}=\frac{1}{f_2}` .....(ii)
Adding Eqs. (i) and (ii), we get
`\frac{1}{v}-\frac{1}{u}=\frac{1}{f_1}+\frac{1}{f_2}`
If the two lens-system is regarded as equivalent to a single lens of focal length f, we have
`\frac{1}{v}-\frac{1}{u}=\frac{1}{f}`
so that we get
`\frac{1}{f}=\frac{1}{f_1}+\frac{1}{f_2}`
The derivation is valid for any number of thin lenses in contact.
Power of a Lens
The power of a lens is defined as the reciprocal of the focal length in meters. SI unit of power of lens is Diopter (D).
`P=\frac{1}{f}`
If several thin lenses of power P1, P2, P3,... are in contact, the effective power of their combination is given by
`P=P_{1}+P_{2}+P_{3}+...`
Dispersion
When white light is incident on a prism, different colors having different wavelengths suffer different deviations. The phenomenon of splitting light into its component colours is known as dispersion. The pattern of colour components of light (VIBGYOR) is called the spectrum of light. The deviation produced by a thin prism depends on the refractive index.
Angular Dispersion
Angular dispersion produced by a prism for white light is the difference in the angles of deviation for two extreme colours i.e. violet and red. It is given by
θ = δV - δR
θ = (nV - nR)A
Dispersive Power
The dispersive power of a prism is defined as the ratio of angular dispersion to the mean deviation produced by the prism.
Dispersive power `\omega=\frac{\delta_{V}-\delta_{R}}{\delta_{Y}}`
Some Natural Phenomena Due to Sunlight
(i). Scattering of Light
The change in direction of light by the particles of the medium through which light passes is known as scattering. As sunlight travels through the earth's atmosphere it gets scattered by the atmospheric particles.
(ii). Rayleigh Law of Scattering
The amount of scattering is inversely proportional to the fourth power of the wavelength. Therefore, the light of shorter wavelengths is scattered much more than light of longer wavelengths.
scattering`\propto\frac{1}{\lambda^4}`
(iii). Blue Sky
Blue has a shorter wavelength than red and is scattered much more strongly. In fact, violet is scattered even more than blue having a shorter wavelength. But since our eyes are more sensitive to blue than violet, we see the sky blue.
(iv). Reddish appearance of the sun in full moon near the horizon
At sunrise and sunset sun rays pass through a larger distance through the atmosphere so most of the blue and other shorter wavelengths are removed by scattering. The least scattered light reaches our eyes and the sun seems reddish.
Optical Instruments
(i). The Eye
Light enters the eye through the cornea a curved front surface. It passes through the pupil which is the central hole in the iris. The size of the pupil can change under the control of muscles. The light is further focussed by the eye lens on the retina. The retina is a film of nerve fibers covering the curved black surface of the eye. The retina contains rods and cones which sense light intensity and colour respectively and transmit electrical signals via the optic nerve to the brain.
The shape (curvature) and therefore the focal length of the lens can be modified somewhat by ciliary muscles. So images are formed at the retina for objects at all distances. This property of the eye is called accommodation.
The closest distance for which the eye lens can focus light on the retina is called the least distance of distinct vision or the near point. The standard value for normal vision is taken as 25 cm (Symbol D). If the object is too close to the eye; the lens cannot curve enough to focus the image on the retina, and the image is blurred.
# Near sightedness or Myopia
The light from a distant object arriving at the eye lens may get converged at a point in front of the retina. This defect is known as nearsightedness or myopia. A concave lens is used to correct the defect.
# Farsightedness or Hypermetropia
If the eye lens focuses the incoming light from a distant object at a point behind the retina, then the defect is called farsightedness or hypermetropia. A convergent lens is needed to compensate for the defect in vision.
# Astigmatism
This occurs when the cornea is not spherical in shape. It may have large curvature in the vertical plane than in the horizontal plane. It results in lines in one direction being well focussed while those in a perpendicular direction may appear distorted.
(ii). The microscope
A simple magnifier or microscope is a converging lens of a small focal length. The lens nearest the object, called the objective, forms a real, inverted, magnified image of the object. This serves as the object for the second lens, the eyepiece, which functions essentially as a simple microscope or magnifier, producing an enlarged virtual final image.
The first inverted image is thus near (at or within) the focal point of the eyepiece, at a distance appropriate for final image formation at infinity, or a little closer for image formation at the near point. Clearly, the final image is inverted with respect to the original object.
Magnification power is given by
`m=\frac{v_0}{u_o}[\frac{D}{v}+\frac{D}{f_e}]`
(iii). Telescope
The telescope is used to provide angular magnification of distant objects. It also consists of an objective and an eyepiece. But here, the objective has a large focal length and a much larger aperture than the eyepiece. Light from a distant object enters the objective and a real image is formed in the tube at the second focal point of the convex objective lens. The eyepiece magnifies this image producing a final inverted image.
Magnifying power is given by
`m=-f_{0}[\frac{1}{f_e}+\frac{1}{v}]`
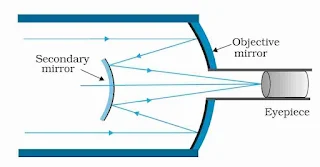
(iv). Reflecting Telescope
One such arrangement using a convex secondary mirror to focus the incident light, which now passes through a hole in the objective primary mirror, is known as a reflecting telescope or a Cassegrain telescope.
Advantages of taking mirror objectives are
There is no chromatic aberration in a mirror.
If a parabolic reflecting surface is chosen, spherical aberration is also removed.
Mechanical support is much less of a problem since a mirror weighs much less than a lens of equivalent optical quality and can be supported over.
The entire back surface not just over rim, unlike lens.
Summary
Reflection is governed by the equation ㄥi = ㄥr and refraction by Snell’s law, sin i / sin r = n.
The critical angle of incidence ic for a ray incident from a denser to a rarer medium is that angle for which the angle of refraction is 90°.
Cartesian sign convention:
1. Distances measured in the same direction as the incident light are positive.
2. Those measured in the opposite direction are negative.
3. All distances are measured from the pole/optic centre of the mirror/lens on the principal axis.
4. The heights measured upwards above the x-axis and normal to the principal axis of the mirror/lens are taken as positive.
5. The heights measured downwards are taken as negative.
Mirror equation: where u and v are object and image distances, respectively and f is the focal length of the mirror.
Lens makers formula.
`\frac{1}{f}=(\mu-1)[\frac{1}{R_1}-\frac{1}{R_2}]`
Dispersion is the splitting of light into its constituent colors.
The Eye: The eye has a convex lens with a focal length of about 2.5 cm. This focal length can be varied somewhat so that the image is always formed on the retina. This ability of the eye is called accommodation. In a defective eye,
- if the image is focussed before the retina (myopia), a diverging corrective lens is needed.
- if the image is focussed beyond the retina (hypermetropia), a converging corrective lens is needed.
- Astigmatism is corrected by using cylindrical lenses.
Magnifying power m of a simple microscope is given by m = 1 + (D/f), where D = 25 cm is the least distance of distinct vision and f is the focal length of the convex lens.
Magnifying power m of a telescope is the ratio of the β angle subtended at the eye by the image to the angle α subtended at the eye by the object. m = β / α.