Wave Optics Class 12 notes Physics Chapter 10
Introduction
In this chapter you will get to know that light does not always travel in a straight line, indeed light is a wave. It interferes, it diffracts and it even undergoes polarization. This new branch of Physics that deals with the wave nature of light is called “Wave Optics”.
Models of Light
(i). Corpuscular model
According to this model, a luminous body emits a stream of particles in all directions. The particles are assumed to be very very tiny. It explained the laws of reflection and refraction of light at an interface using concepts of elastic collisions and momentum conservation. Although this law could explain reflection and refraction, this law could not satisfactorily explain a phenomenon like interference, polarization, and diffraction. In 1637, Descartes gave the corpuscular model of light.
(ii). Wave model
The wave theory of light was first put forward by Christian Huygen in 1678. On the basis of his wave theory, Huygen explained satisfactorily the phenomenon of reflection, refraction, and total internal reflection.
Huygens’ Principle
According to this principle,
Each point of a wavefront is a source of secondary disturbance and the wavelets emanating from these points spread out in all directions with the speed of the wave.
The envelope of these wavelets gives the shape of the new wavefront.
If we draw a common tangent to all these spheres, then we obtain an envelope which is again a sphere centered at the point source.
Recommended Books
- NCERT Textbook For Class 12 Physics Part 1 & 2
- CBSE All In One Physics Class 12 2022-23 Edition
- Oswaal CBSE Chapterwise Question Bank Class 12 Physics Book
- Modern's abc Plus of Physics for Class-12 (Part I & II)
Read also: Dual Nature of Radiation and Matter Class 12 Physics Notes Chapter 11
Application of Huygens’ Principle
(i). Reflection of a Plane Wave
Let us consider a plane wave AB incident at an angle 'i' on a reflecting surface MN.
Time taken by the wave to advance to point C from point B will be t.
Hence BC = vt
Let EC represent a tangent drawn from C to wavefront from E to the spherical wavefront.
AE = vt
Consider, ΔAEC and ΔABC
AC = AC (Common side)
∠AEC = ∠ABC (Each 90°)
AE = BC (Each vt)
Hence, ΔAEC ≅ ΔABC
∠i = ∠r
which proves the law of reflection.
Read also: Haloalkanes and Haloarenes Chemistry Class 12 Notes Chapter 10
(ii). Refraction of a Plane Wave
Let v1 and v2 represent the speed of light in medium-1 and medium-2 respectively. Consider a plane wavefront AB propagating in the direction AA', incident on the medium boundary at point A at an angle of incidence 'i'. Let t be the time taken to travel from B to C.
BC = v1t
From point A, draw a sphere of radius v2t, let CE represent the forward tangent plane. It is refracted wavefront at t.
AE = v2t
From ΔABC, `sin i=\frac{BC}{AC}=\frac{v_{1}t}{AC}` .....(i)
From ΔAEC, `sin r=\frac{AE}{AC}=\frac{v_{2}t}{AC}` .....(ii)
Dividing (i) by (ii), we have
`\frac{sin i}{sin r}=\frac{v_{1}t}{v_{2}t}`
`\frac{sin i}{sin r}=\frac{v_{1}}{v_{2}}`
which proves law of refraction.
Wavefront
A wavefront is a continuous locus of all those points in a medium that oscillate in the same phase. The physical view of a wavefront is the ripples on a water surface. When a stone is dropped in a water pond, the disturbance travels radially outward and what you see are circular wave-fronts traveling outward.
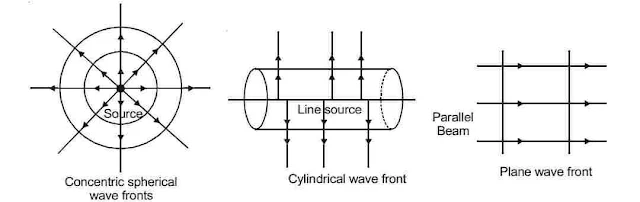
Types of Wavefront
Depending on the mode of propagation of light or the source, the wave fronts can be converging, diverging, or plane. For a point source, spherical diverging wavefronts are formed. For an extended line source, cylindrical diverging wavefronts are formed. For a source at infinity, a plane wavefront exists.
Read also: Conceptual Questions for Class 12 Physics Chapter 10 Wave Optics
The Doppler’s Effect
When light-producing source moves away from the observer the frequency as measured by the observer will be smaller than that is actually generated by the source. Astronomers call the increase in wavelength due to the Doppler effect redshift.
When an observer moves toward the source or the source move towards the observer, then apparent wavelength decreases and the visible spectrum appears to be shifted towards a shorter wavelength. Hence, we call this a blue shift.
Coherent and Incoherent Sources of Light
(i). Coherent sources
Two sources of light that continuously emit light waves of the same frequency (or wavelength) with a zero or constant phase difference between them are called coherent sources. Ex- LASER.
(ii). Incoherent sources
Two sources of light that do not emit light waves with a constant phase difference are called incoherent sources. Ex- Two different light sources produce incoherent waves.
Interference of Light Wave
Interference is the phenomenon in which two waves superpose to form the resultant wave of the lower, higher, or same amplitude. When the crest of one wave falls on the crest of another wave such that the amplitude is maximum then interference is called constructive interference. When the crest of one wave falls on the trough of another wave such that the amplitude is minimum then interference is called destructive interference.
Conditions for sustained interference
Two sources of light must be coherent.
The frequencies (or wavelength) of the two waves should be equal.
The light must be monochromatic.
The amplitudes of the interfering waves must be equal or nearly equal.
The two sources must be narrow.
Young’s Double Slit Experiment
In the diagram, S1 and S12 are narrow slits that are parallel to each other. As S is narrow, it diffracts the light that falls on it and illuminates both S1 and S2. Interference occurs in the region where the light from S1 overlaps that from S2. A series of alternately bright and dark bands can be observed on a screen placed in this region of overlap.
For a point P on the screen, the path difference,
`S_{2}P-S_{1}P=d sin\theta` .....(i)
For very small θ,
`sin\theta\approx tan\theta=\frac{y}{D}` ....(ii)
The phase difference between the waves at P = ф
`ф =\frac{2\pi}{\lambda}[S_{2}P-S_{1}P]` ....(iii)
`ф =\frac{2\pi}{\lambda}(\frac{dy}{D})`
For constructive interference,
ф = 2nπ (n = 0, 1, 2, ....)
`\frac{2\pi}{lambda}(\frac{dy}{D})=2\pi n`
`y=n\frac{\lambda D}{d}`
Similarly for destructive interference,
`y=(2n-1)\frac{\lambda D}{d}(n=1, 2, ....)`
Fringe width
`\beta=y_{n+1}-y_{n}`
`\beta=\frac{\lambda D}{d}`
Diffraction
The phenomenon of bending light around the corners of an obstacle is called the diffraction of light.
Difference between Diffraction and Interference
| S.No. | Interference | Diffraction |
| 1. | Interference may be defined as waves emerging from two different sources, producing different wavefronts. | Diffraction, on the other hand, can be termed as secondary waves that emerge from the different parts of the same wave. |
| 2. | The intensity of all the points on maxima is of similar intensity in interference. | In diffraction, there is a variance of the intensity of positions. |
| 3. | It is absolutely dark in the region of minimum intensity, in the case of interference. |
We see a variance in the intensity of interference in diffraction. |
| 4. | The width of the fringes in interference is equal in interference. | The width of the fringes is not equal in interference. |
| 5. | The sources are referred to as interference sources if the number of sources is as few as two sources. | If the number of sources is more than to the sources are referred to as diffraction sources. |
Polarisation
If the vibrations of a wave are present in just one direction in a plane perpendicular to the direction of propagation, the wave is said to be polarised or plane polarised. The phenomenon of restricting the oscillations of a wave to just one direction in the transverse plane is called the polarization of waves.
Malus' Law
It states that the intensity of plane-polarized light that passes through an analyzer varies directly with the square of the cosine of the angle between the plane of the polarizer and the transmission axes of the analyzer.
`I=I_{0}cos^{2}\theta`
Polariser
A device that polarises the unpolarised light passed through it is called a polariser.
Optical Activity
When plane polarised light passes through certain substances, the plane of polarization of the light is rotated about the direction of propagation of light through a certain angle. This phenomenon is called optical activity or optical rotation and the substances are optically active.
Methods of producing plane polarised light
(i). Polarisation by reflection
When a light wave is incident on a boundary of a medium, a part of a light wave is reflected back into the medium from which it is incident and a part of the wave is refracted into the other medium.
When unpolarized light is incident on the boundary between two transparent mediums, for an angle of incidence in which the reflected wave travels at a right angle to the refracted wave, the reflected light is polarized while the refracted light is partially polarized.
Brewster’s Law
According to Brewster’s law, When unpolarized light is incident on a transparent substance surface, it experiences maximum plan polarization at the angle of incidence whose tangent is the refractive index of the substance for the wavelength.
`n=tan i` (where i = incident angle)
Q. Show that reflected and refracted beams are mutually perpendicular when the angle of incidence is equal to the polarizing angle.
By Snell's Law
`n=\frac{sin i}{sin r}` .....(i)
By Brewster’s Law
`n=tan i` .....(ii)
From eq. (i) and (ii)
`\frac{sin i}{sin r}=tan i`
`\frac{sin i}{sin r}=\frac{sin i}{cos i}`
`sin r=cos i`
`sin r=sin (90-i)`
`r=90-i`
`i+r=90`
(ii). Polarization by Scattering
When light is incident on the small particles of the atmosphere such as dust, and air molecules it is absorbed by the electrons in the molecules, hence electrons start vibrating. These vibrating electrons emit radiations in all directions except in their own line of vibration. The emitted radiations (light) scattered in a direction perpendicular to the direction of incident light are plane polarised. The light in all other directions is partially polarised.
Summary
Wavefront: It is defined as the continuous locus of all the principles of a medium, which are vibrating in the same phase.
Huygen’s principle:
1. Every point on the given wave front acts as a fresh source of new disturbance, called secondary wavelets, which travel in all directions with the velocity of light in the medium.
2. A surface touching these secondary wavelets, tangentially in the forward direction at any instant gives the new wavefront at that instant. This is called secondary wavefront.
Superposition principle: When two or more wave motions traveling through a medium superimpose one other, a new wave is formed in which resultant displacement at any instant is equal to the vector sum of the displacement due to individual waves.
Interference: Interference of light is the phenomenon of redistribution of light energy in a medium on account of the superposition of light waves from two coherent sources.
Coherent sources: The source of light, which emit continuous light waves of the same wavelength, same frequency, and in the same phase or have a constant phase difference are called coherent sources.
Huygens’ principle tells us that each point on a wavefront is a source of secondary waves, which add up to give the wavefront at a later time. Young’s double-slit of separation d gives equally spaced fringes of angular separation λ/d.
Natural light, e.g., from the sun is unpolarized. This means the electric vector takes all possible directions in the transverse plane.
Polarised light can also be produced by reflection at a special angle (called the Brewster angle) and by scattering through π/2 in the earth’s atmosphere.