Moving Charges and Magnetism Class 12 Notes Physics Chapter 4

Introduction

In the previous chapters, we discussed how a charged object produces an electric field. Similarly, a magnet produces the magnetic field at all points in space around it. You get a hint of that magnetic field whenever you attach a note to the refrigerator door with a small magnet, or accidentally erase a computer disk by bringing it near a magnet.

In this chapter, we will discuss all this magnetic field (`\vec{B}`) and the force exerted by this magnetic field on moving charged particles.

Magnetic Field

Moving Charges and Magnetism Class 12 Notes

We have discussed that a stationary charge creates an electric field in its surrounding space, similarly, a moving charge creates a field in its surrounding space which exerts a force on a moving charge this field is known as a magnetic field which is a vector quantity and represented by B.

The motion of charged particles in a Magnetic Field

When a charged particle q is thrown in a magnetic field `\vec{B}` with a velocity `\vec{v}` then the force acting on the particle is given by F = qvB.sinθ, where θ is the angle between the velocity and the magnetic field. As the magnetic force on a charged particle is perpendicular to the velocity, it does not do any work on the particle. Hence, the kinetic energy or the speed of the particle doesn’t change due to the magnetic force.

Case I : θ = 0° or 180°

The path followed: A straight line

If a charged particle is thrown parallel or antiparallel to the magnetic field it does not experience any magnetic force as the angle θ between v and B will be zero or 180°. So it will continue to move in a straight line with constant velocity.

Case II : θ = 90°

The path followed: Circular

When a charged particle is projected perpendicular to a uniform magnetic field, its path is a circle. The magnetic Lorentz force acts as the centripetal force causing the charged particle to move in a circular path of radius R with constant speed.

`F=qvB=\frac{mv^2}{R}`

`\Rightarrow R=\frac{mv}{qB}`

Angular velocity `(\omega)=\frac{v}{R}=\frac{qB}{m}`

Time period of revolution `T=\frac{2\pi}{\omega}=\frac{2\pi m}{qB}`

Frequency of revolution `=\frac{1}{T}=\frac{qB}{2\pi m}`

Recommended Books

Biot-Savart Law

Consider an infinitesimal element dl of the conductor. The magnetic field dB due to this element is to be determined at a point P which is at a distance r from it. Let θ be the angle between dl and the position vector r. The direction of dl is the same as the direction of the current.

According to Biot-Savart law, the magnitude of the magnetic field dB is proportional to the current I, and the element length dl is inversely proportional to the square of the distance r. Its direction is perpendicular to the plane containing dl and r. Thus in vector notation,

`d\vec{B}\propto\frac{Id\vec{l}sin\theta}{r^2}`

`d\vec{B}=\frac{\mu_0}{4\pi}\frac{Id\vec{l}sin\theta}{r^2}`

Where `\frac{μ_0}{4π}` is a constant of proportionality. The above expression holds when the medium is a vacuum. The proportionality constant in the SI unit has a value, `\frac{μ_0}{4π}=10^{-7}` T-m/A. We call `μ_0` the permeability of free space.

Magnetic Field due to a Loop of Current

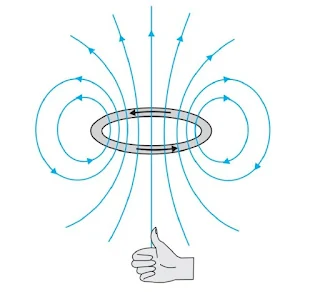
Magnetic field lines due to a loop of wire are shown in the figure. The direction of the magnetic field on the axis of the current loop can be determined by the right-hand thumb rule. If the fingers of the right hand are curled in the direction of the current, the stretched thumb is in the direction of the magnetic field.

Consider a current loop placed in a plane carrying current i in an anticlockwise sense. Due to a small current element i.dl shown in the figure, the magnetic field is given by

`dB=\frac{\mu_0}{4\pi}\frac{idl.sin90}{r^2}`

Strength of Magnetic Field at the center of loop,

`\int dB=\int\frac{\mu_0}{4\pi}\frac{idl.sin90}{r^2}`

`B=\frac{\mu_0}{4\pi}\frac{i.sin90}{r^2}\int dl`

`B=\frac{\mu_0}{4\pi}\frac{i}{r^2}2\pi r`

`B=\frac{\mu_{0} i}{2r}`

If the loop has n round of wire,

`B=\frac{\mu_{0}n i}{2r}`

Relation between μ₀ and ε₀

`\frac{1}{4\pi\epsilon_0}=9\times10^{9}` .....(1)

`\frac{\mu_0}{4\pi}=10^{-7}` .....(2)

Dividing by eq. (2) to eq. (1)

`\frac{\frac{\mu_0}{4\pi}}{\frac{1}{4\pi\epsilon_0}}=\frac{10^{-7}}{9\times10^9}`

`\frac{\mu_0}{4\pi}\times\frac{4\pi\epsilon_0}{1}=\frac{1}{9\times10^{9+7}}`

`\mu_0 \epsilon_0=\frac{1}{9\times10^{16}}`

`\mu_0 \epsilon_0=\frac{1}{(3\times10^{8})^2}`

`\mu_0 \epsilon_0=\frac{1}{c^2}`

`c=\frac{1}{\sqrt{\mu_0\epsilon_0}}`

Ampere’s Circuital Law

Ampere’s circuital law states that the line integral of a steady magnetic field over a closed loop is equal to μ₀ times the total current (I_e) passing through the surface bounded by the loop i.e.,

`\int B.dl=\mu_0 I_e` where I_e is enclosed current

Applications of Ampere’s Circuital Law

(i). Magnetic Field Due to a Straight Infinite Current-Carrying Wire

Consider a straight infinite current-carrying wire. We draw an Amperian loop, a circle of radius r with wire as its axis. The Amperian loop exploits the symmetry of the situation as the magnetic field is tangential at every point in the loop. The magnetic field has equal magnitude at all the points.

Now using the Ampere's Law

`\int B.dl=\mu_0 I`

`\int Bdl.cos0=\mu_0 I`

`B\int dl=\mu_0 I`

`B(2\pi r)=\mu_0 I`

`B=\frac{\mu_0 I}{2\pi r}`

(ii). Magnetic field due to a long solenoid

A solenoid is a tightly wound helical coil of wire. If the length of the solenoid is large, as compared to its radius, then in the central region of the solenoid, a reasonably uniform magnetic field is present. The figure shows a part of the long solenoid with a number of turns (n).

We can find the field by using Ampere circuital law. Consider a rectangular loop ABCD and we choose direction of integration to be anti-clockwise. For this loop

`\int_{ABCD} B.dl=\mu_0 I`

`\int_{ABCD} B.dl=\int_{AB} B.dl+\int_{BC} B.dl+\int_{CD} B.dl+\int_{DA} B.dl`

`\int_{ABCD} B.dl=0+\int_{BC} B.dl+0+0`

`\int_{ABCD} B.dl=B\times a`

If the solenoid has n round of wire in unit length then current is given by

I = nai

B x a = μ₀ (nai)

B = μ₀ ni

Magnetic Force

It is observed that when the charge is at rest it experiences almost no force. However, if the charge q is given a velocity v in the direction of the current, it is deflected towards the wire. Hence we conclude that the magnetic field exerts a force on a moving charged particle. The combination of the electric and magnetic force on a point charge is known as Lorentz Force.

Consider a point charge q moving with velocity v located at position vector r at a given time t. If an electric field E and a magnetic field B exist at that point, then force on the electric charge q is given by

`\vec{F}=q[\vec{E}+\vec{v}\times\vec{B}]`

This force was first given by H. A. Lorentz, hence it is called the Lorentz force.

Fleming’s left-hand rule

If we stretch the thumb and first two fingers of our left hand in mutually perpendicular directions such that the forefinger points along B and the middle finger points along with v, then the thumb points along with F.

Magnetic Force on a Current-Carrying Conductor

Suppose a conducting wire carrying a current i is placed in a uniform magnetic field B. The length and the cross-sectional areas are l and A respectively. The free electrons in the wire are moving with drift velocity v_d opposite to the direction of the current.

Force experienced by each electron

`\vec{F}=e(\vec{v_{d}}\times\vec{B})`

Total force experienced by the conductor is

`\vec{F_m}=(Number-of-e)[e(\vec{v_{d}}\times\vec{B})]`

`\vec{F_m}=(nlA)e(\vec{v_{d}}\times\vec{B})`

`\vec{F_m}=(n e A\vec{v_{d}})(\vec{l}\times\vec{B})`

`\vec{F_m}=i(\vec{l}\times\vec{B})`.....`[\because n e A\vec{v_{d}}=i]`

Force between two parallel current carrying wires

The figure shows two parallel wires carrying currents i₁ and i₂ in the same direction. Each conductor produces a magnetic field at the position of the other. This magnetic field exerts a force on the other conductor. As shown, the conductors attract each other when current flows in the same sense through them.

Here, we shall assume that the conductors are infinitely long and we shall determine the force per unit length between the conductors.

Let B₁ be the magnetic fields due to 1st conductors.

`\therefore B_{1}=\frac{\mu_{0}i_1}{2\pi r}`

Force on a section of length l for conductor 2 is

`F_{21}=i_{2}lB_{1}sin90`

`F_{21}=\frac{\mu_{0}i_{1}i_{2}}{2\pi r}l`

`\frac{F_{21}}{l}=\frac{\mu_{0}i_{1}i_{2}}{2\pi r}`

The two conductors attract each other by a force per unit length `\frac{\mu_{0}i_{1}i_{2}}{2\pi r}`

Current Loop as a Magnetic Dipole

A current-carrying loop behaves like a magnetic dipole. It has two poles viz north and south like that of a bar magnet. The following figures show magnetic field lines due to a bar magnet and a current-carrying loop.

The magnetic dipole moment vector for a current loop is given by `\vec{M} = Ni\vec{A}` ,

where N = number of loops or turns

i = current through each turn

A = area of each turn

Torque on a Current Loop in a Uniform Magnetic Field

A current loop ABCD is placed in a uniform magnetic field B. The dimensions are AB = l and BC = b. The plane of the loop makes an angle θ with a magnetic field. M is magnetic dipole moment. The angle between M and B is θ.

The four straight sections AB, BC, CD and DA experience forces due to the magnetic field. F represents the magnitude of the force on AB and CD while F′ represents the magnitude of forces on AD and BC. The directions are shown in the figure.

F₁ = F₂ = i l B sin90

F₁ = F₂ = i l B

Clearly, the net force is zero. But the forces on AB and CD constitute a couple. The torque due to them is τ = F × perpendicular distance between the lines of action.

⇒ τ = F × bsinθ

τ = i l B bsinθ

τ = i(l b) B sinθ

τ = iA B sinθ

τ = MB sinθ

τ = M x B

Cyclotron

A cyclotron is a machine to accelerate charged particles or ions to high energies. The cyclotron uses both electric and magnetic fields in combination to increase the energy of charged particles. As the fields are perpendicular to each other they are called crossed fields. The Cyclotron uses the fact that the frequency of revolution of the charged particle in a magnetic field is independent of its energy and speed.

The particles move most of the time inside two semicircular disc-like metal containers, D₁ and D₂, which are called dees as they look like the letter D. Figure shows a schematic view of the cyclotron. Inside the metal boxes, the particle is shielded and is not acted on by the electric field. The magnetic field, however, acts on the particle and makes it go round in a circular path inside a dee. Every time the particle moves from one dee to another it is acted upon by the electric field. The sign of the electric field is changed alternately in tune with the circular motion of the particle.

This ensures that the particle is always accelerated by the electric field. Each time the charge enters the gap, the electric field increases the energy of the particle. As energy increases, the radius of the circular path increases. So the path is a spiral one.

The whole assembly is evacuated to minimize collisions between the ions and the air molecules. A high-frequency alternating voltage is applied to the dees. In the sketch shown in the figure, positive ions or positively charged particles (e.g., protons) are released at the center P. They move in a semicircular path in one of the dees and arrive in the gap between the dees in a time interval T/2; where T is the period of revolution, given by

`T=\frac{1}{f_c}=\frac{2\pi m}{qB}`

`f_{c}=\frac{qB}{2\pi m}`

This frequency is called the cyclotron frequency for obvious reasons and is denoted by f_c.

The frequency f_a of the applied voltage is adjusted so that the polarity of the dees is reversed at the same time that it takes the ions to complete one-half of the revolution. The requirement f_a = f_c is called the resonance condition. The phase of the supply is adjusted so that when the positive ions arrive at the edge of D₁, then D₂ is at a lower potential and the ions are accelerated across the gap. Inside the dees, the particles travel in a region free from the electric field.

The increase in their kinetic energy is qV each time they move from one dee to another. As the radius is directly proportional to speed, the radius of their path goes on increasing each time their kinetic energy increases. The ions are repeatedly accelerated across the dees until they have the required energy to have a radius approximately that of the dees. They are then deflected by a magnetic field and leave the system via an exit slit. We have

`v=\frac{qBR}{m}`

where R is the radius of the trajectory at exit and equals the radius of a dee.

Hence, kinetic energy of the ions is,

`\frac{1}{2}mv^2=\frac{q^{2}B^{2}R^{2}}{2m}`

The operation of a cyclotron is based on the fact that the time for one revolution of an ion is independent of its speed or radius of its orbit.

The cyclotron is used to bombard nuclei with energetic particles and study the resulting nuclear reactions. It is also used to implant ions into solids and modify their properties or even synthesize new materials. It is used in hospitals to produce radioactive substances which can be used in diagnosis and treatment.

The Moving Coil Galvanometer

The galvanometer consists of a coil, with many turns free to rotate about a fixed axis, in a uniform radial magnetic field. The coil is wrapped on a cylindrical soft iron core which enables the field to remain radial in all positions of the coil.

When a current flows through the coil, a torque acts on it.

`\vec{\tau}=\vec{M}\times \vec{B}`

`\tau=NIAB sin\theta`

Here the symbols have their usual meaning. A spring Sp provides a counter torque Kφ that balances the magnetic torque NIAB, resulting in a steady angular deflection φ. In equilibrium

Kφ = NIAB

where K is a torsional constant of the spring, that is restoring torque per unit twist. The deflection is indicated on the scale by a pointer attached to the spring. We have

`φ =(\frac{NAB}{K})I`

The quantity in brackets is a constant for a given galvanometer.

Galvanometer as Ammeter

The galvanometer cannot as such be used as an ammeter to measure the value of the current in a given circuit. This is for two reasons.

A galvanometer is a very sensitive device. It gives a full-scale deflection for a current of the order of μA.
For measuring currents, the galvanometer has to be connected in series, and as it has a large resistance, this will change the value of the current in the circuit.

To overcome these difficulties, one attaches a small resistance r_s called shunt resistance, in parallel with the galvanometer coil, so that most of the current passes through the shunt. The resistance of this arrangement is

`\frac{R_{G}r_{s}}{R_{G}+r_s}=r_s`

We define the current sensitivity of the galvanometer as the deflection per unit current. Thus

`\frac{\phi}{i}=\frac{NAB}{K}`

Galvanometer as Voltmeter

To use a galvanometer to find the potential difference between a section of a circuit, it must be connected in parallel to that section of the circuit. Further, it must draw a very small current, otherwise, the voltage measurement will disturb the original setup by an amount that is very large. Usually, we like to keep the disturbance due to the measuring device below one percent. To ensure this, a large resistance R is connected in series with the galvanometer.

We define voltage sensitivity as the deflection per unit voltage

`\frac{\phi}{V}=(\frac{NAB}{K})\frac{i}{V}`

Summary

Lorentz force: When a charged particle moves in a combined magnetic and electric field then the force acting on it is known as Lorentz force. `\vec{F}= q(\vec{v}\times \vec{B}+\vec{E})`
Pitch of a helix: It is defined as the distance traveled along the axis of the helix in one complete rotation.
Cyclotron: It is a device to accelerate charged particles. It uses both electric and magnetic fields. The speed of particle is increased by an electric field.
Magnetic dipole moment: All current carrying loops behaves as magnetic dipoles. Magnetic moment M is written as `\vec{M}=i\vec{A}`, where A is the area vector pointing normally to the plane of the loop.
Biot-Savart Law: Magnetic field produced by a current-carrying element is proportional to the current I, the element length dl and inversely proportional to the square of the distance r. In vector form
`d\vec{B}=\frac{μ_0}{4π}I\frac{dl×r}{r^3}`
Ampere’s circuital law: The line integral of the magnetic field over a closed-loop equals μ₀ times the current enclosed by the loop.
`\int\vec{B}d\vec{l}=μ_{0}i_{e}`
Moving coil galvanometer: It is a device that gives deflection when a current is passed through it. It can be used to measure currents and voltages by applying appropriate shunt resistance.
Current sensitivity: It is defined as the deflection produced per unit of current passed through the galvanometer.
Voltage sensitivity: It is defined as the deflection produced per unit voltage applied across the galvanometer.
Parallel currents attract and anti-parallel currents repel.
A moving coil galvanometer can be converted into an ammeter by introducing a shunt resistance r_s, of small value in parallel. It can be converted into a voltmeter by introducing a resistance of a large value in series.

M-Physics Tutorial

Moving Charges and Magnetism Class 12 Notes Physics Chapter 4

Introduction

Magnetic Field

The motion of charged particles in a Magnetic Field

Recommended Books