Debye shielding in Plasma Physics
▶Debye shielding
The Debye length is a most important physical parameter for the description of a plasma. It provides a measure of the distance at which the effect of the electric field of an individual charged particle is felt by other charged particles inside the plasma.
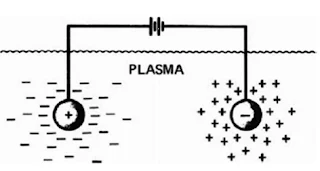 |
| Debye Shielding |
The charged particles arranged themselves in such a way as to effectively shield any electrostatic field within some distance of the order of Debye length. This shielding of the electrostatic field is a result of the collective effects of plasma particles.
The shielding distance was first calculated by Debye for an electrolyte. It can be shown that Debye length (λD) is directly proportional to the square root of temperature (T) and inversely proportional to the square root of the number of electron (n).
`\lambda_D=\left(\frac{\in_\circ kT}{n.e^2}\right)^{1/2}`
Where, Ꜫ0 = permittivity of free space
k = Boltzmann constant
e = Charge of electron
The Debye length can also be considered as a measure of the distance in which electric potentials can fluctuate in a plasma, which can be converted into electrostatic potential energy as thermal particle kinetic energy. The number of electrons (ND) inside a Debye sphere is given by
`N_D=4/3πλ_{ D}^3\ n`
`N_D=4/3\pi\left(\frac{\in_\circ\kT}{\n^{1/3}.\ e^2}\right)^{3/2}`
The Debye shielding effect is a feature of all plasmas, although this does not occur in every medium that contains charged particles. An essential and obvious requirement for the existence of plasma is that the physical dimensions of the system are larger than the Debye length (λD). Otherwise, there is just not sufficient space for the collective shielding effect to take place, and the collection of charged particle will not exhibit plasma behaviour.
The quantity Defined by (g = 1 / nλD3) is known as the plasma parameter and the condition g << 1 is called the plasma approximation. This parameter is also a measure of the ratio of the mean inter-particle potential energy to the mean plasma kinetic energy.

