Mechanical Properties of Fluids Class 11 notes Physics Chapter 10
Introduction
In this chapter, we shall study some common physical properties of liquids and gases. How are fluids different from solids? What is common in liquids and gases? Unlike a solid, a fluid has no definite shape of its own. Solids and liquids have a fixed volume, whereas a gas fills the entire volume of its container.
Liquids and gases can flow and are therefore, called fluids. Earth has an envelop of air and two-thirds of its surface is covered with water. All the processes occurring in living beings including plants are mediated by fluids.
Pressure
We can define pressure as the normal force acting per unit area of a surface. It is denoted by P and SI unit of it is pascal (Pa). It is a scalar quantity.
`P=\frac{F}{A}`
We observe that the same force (weight) exerts different pressures for different areas in contact. Lesser the area, more is the pressure exerted for a given force.
Density
The density of any material is defined as its mass per unit its volume. If a fluid of mass m occupies a volume V, then its density is given as
`Density=\frac{m}{V}`
Density is usually denoted by the symbol ρ. It is a positive scalar quantity. Its SI unit is kg m–3 and its dimensions are [ML–3].
Recommended Books
- NCERT Textbook For Class 11 Physics Part 1 & 2
- CBSE All In One Physics Class 11 2022-23 Edition
- Oswaal CBSE Chapterwise Question Bank Class 11 Physics Book
- Modern's abc Plus of Physics for Class-11 (Part I & II)
Read also: Thermal Properties of Matter Class 11 Physics Notes Chapter 11
Pascal’s Law
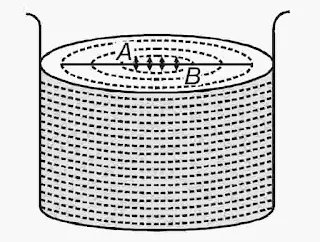
This law states that the pressure in a fluid at rest is same at all points which are at the same height.
Imagine a small element of fluid in the shape of a right angled prism. All its points lie at the same depth inside the liquid. Therefore the effect of gravity is same at all these points. The forces exerted by rest of the fluid on different surfaces of this fluid element are as follows:
`F_{1}=F_{2}=F_{3}`
If A1, A2 and A3 are the surface areas of faces respectively, then by dividing.
`\frac{F_1}{A_1}=\frac{F_2}{A_2}=\frac{F_3}{A_3}`
`p_{1}=p_{2}=p_{3}`
So, the pressure exerted is same in all directions in a fluid at rest, at the points at equal height.
Read also: The s-Block Elements Class 11 Notes Chemistry Chapter 10
Variation of Pressure with Depth
Let’s find the difference in pressures at two points, whose levels differ by a height h in a fluid at rest. Let P1 and P2 be the pressures at two points 1 and 2 inside a fluid. Point 1 is at a height h above the point 2.
Imagine a fluid element in the shape of a cylinder as shown. If A be the area of the top and the bottom of this cylinder, then
`F_{1}=P_{1}A`
`F_{2}=P_{2}A`
Since, the fluid remains at rest, therefore the force F2, which acts upwards should balance the two downward forces. These are, the force F1 exerted at the top of the cylinder, and the weight W of the fluid confined within the cylinder.
`F_{2}=F_{1}+mg`
If ρ is the density of the fluid, then
`F_{2}=F_{1}`+ρ.(volume of the cylinder).g
`P_{2}A=P_{1}A+ρ.(A.h).g`
`P_{2}=P_{1}+ρgh`
`P_{2}-P_{1}=ρgh`
This result tells us that as we go deep down a liquid the pressure goes on increasing. This pressure depends only on the height of the liquid column above the point.
Atmospheric Pressure
The atmospheric pressure at a point is equal to the weight of a column of air of unit cross-sectional area extending from that point to the top of the atmosphere. Its value is 1.013 × 105 Pa at sea level. Atmospheric pressure is measured using an instrument called barometer.
Units os Atmospheric Pressure
SI unit of pressure is N m–2 or Pascal (Pa)
Atmosphere, 1 atm = 1.013 × 105 Pa = 760 mm of Hg
1 torr = 133 Pa
1 mm of Hg = 1 torr
1 bar = 105 Pa
1 millibar = 100 Pa
Read also: Conceptual Questions for Class 11 Physics Chapter 10 Mechanical Properties of Fluid
Gauge Pressure
When we remove atmospheric pressure from total pressure of any system then this remaining pressure is called Gauge Pressure. The excess pressure P–Pa, at depth h is called a gauge pressure at that point.
Archimedes’ Principle
When a body is partially or completely immersed in a liquid, it loses some of its weight. The loss in weight of the body in the liquid is equal to the weight of the liquid displaced by the immersed part of the body. The upward force excerted by the liquid displaced when a body is immersed is called buoyancy. Due to this, there is apparent loss in the weight experienced by the body.
Law of Floatation
A body floats in a liquid if weight of the liquid displaced by the immersed portion of the body is equal to the weight of the body. When a body is immersed partially or wholly in a liquid, then the various forces acting on the body are
Upward thrust (T) acting at the centre of buoyancy and whose magnitude is equal to the weight of the liquid displaced
The weight of the body (W) which acts vertically downward through its centre of gravity.
(a) When W > T, the body will sink in the liquid;
(b) When W = T, then the body will remain in equilibrium inside the liquid;
(c) When W < T, then the body will come upto the surface of the liquid.
Streamline Flow
When a liquid flows such that each particle of the liquid passing a given point moves along the same path and has the same velocity as its predecessor had at that point, the flow is called streamlined or steady flow. The path followed by a fluid particle in steady flow is called streamline.
Equation of Continuity
According to this theorem, "For the streamline flow of an incompressible fluid through a pipe of varying cross-section, product of cross-section area and velocity of streamline flow (Av) remains constant throughout the flow".
Av = constant
Bernoulli’s Principle
It may be stated as follows: As we move along a streamline, the sum of the pressure (P), the kinetic energy per unit volume (`\frac{ρv^2}{2}`) and the potential energy per unit volume (ρgh) remains a constant.
`P+ρgh+\frac{1}{2}ρv^{2}=`constant
Limitations of Bernoulli’s Equation
The equation is valid only for incompressible fluids having streamline flow. It is because it does not take into account the elastic energy of the fluids.
It is assumed that no energy is dissipated due to frictional force exerted by different layers of fluid on each other.
It does not hold for non-steady flow. In such situation velocity and pressure constantly fluctuate with time.
Surface Tension
Surface tension is defined as the surface energy per unit area or the force per unit length acting in the plane of the interface between the plane of the liquid and any other substance. The surface tension of a liquid usually decreases with increase in temperature.
`S=\frac{F}{l}`
Capillary Rise
A tube of very fine bore is called a capillary. ‘Capilla’ is a Latin word which means hair. Thus, capillary is a very thin tube. When such a tube, open at both ends, is dipped in a beaker containing water, water rises in it against gravity.
Let us find an expression for the height h, upto which a liquid rises in a capillary tube. Let a capillary tube of radius r be dipped in a liquid of surface tension S and density ρ.
Thus, capillary rise
`h=\frac{2S cosθ}{rρg}`
If the angle of contact for this liquid and the capillary tube is acute, the liquid forms a concave meniscus.
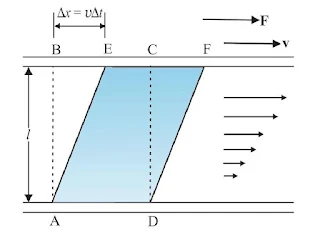
Viscosity
When a fluid moves, it flows in the form of parallel layers. These layers exert a force on each other which tends to oppose their relative motion. This is similar to what a frictional force does when two solids in contact move or tend to move over each other. The property of fluid which gives rise to such frictional force in them, is called viscosity. It is denoted by ‘η’. Its SI unit is N s m–2 or Pa s which is also called poiseuille (Pl). The dimensions of viscosity are [ML–1T–1].
`η=\frac{F}{A{dv}/{dx}}`
where, dv/dx = velocity gardient
F = frictional force between layer of water
A = area of layer
Angle of Contact
The angle of contact is defined as the angle that the tangent to the liquid surface at the point of contact makes with the solid surface inside the liquid. The angle of contact depends on the nature of the solid and the liquid in contact. At the point of contact, the surface forces between the three media must be in equilibrium.
Stokes’ Law
When a spherical ball is dropped in a liquid, he observed that the viscous force F experienced by the ball is proportional to the
– velocity of the object through the fluid, v
– viscosity of the fluid, η
– radius of the sphere, r
Thus F ∝ ηrv
Here, the constant of proportionality is found to be 6π.
Thus F = –6πηrv ← Stokes’ law.
The negative sign in the above expression just indicates that the retarding force is opposite to the direction of motion of the object.
Terminal Velocity
The maximum constant velocity acquired by a body while falling through a viscous medium is called its terminal velocity. It is usually denoted by VT.
When the body acquires terminal velocity,
the upward viscous force + the upward buoyant force = weight of the ball
Reynolds Number
Whether a flow will be turbulent or not, is decided by a dimensionless parameter called Reynolds number Re. This parameter is given by the relation
`R_{e}=\frac{ρvd}{η}`
where, ρ = density of the fluid
v = velocity of the fluid
η = viscosity of the fluid
d = diameter of the pipe through which the fluid flows
If Re < 1000, the flow is streamline or laminar
If Re > 2000, the flow becomes turbulent
If 1000 < Re < 2000, flow is unsteady i.e., it may change from laminar to turbulent and vice versa.
Poiseuille’s Formula
The Poiseuille’s formula gives an expression for volume flow rate through a capillary tube of inner radius r and length l due to a pressure difference between its ends, P. The volume flow rate is represented by Q such that
`Q=\frac{dV}{dt}`
According to Poiseuille’s,
`\frac{dV}{dt}=(\frac{\pi}{8})\times (\frac{P}{l})\times \frac{r^4}{η}`
Here, η is the coefficient of viscosity and all symbols have standard meaning.
Summary
Fluid : A substance that can flow is called fluid. Both liquids and gases are fluids.
Pressure : The normal force acting per unit area of a surface is called pressure.
Density : The density of any material is defined as its mass per unit its volume. Its SI unit is kg / m3.
Relative density : The ratio of the density of a substance to the density of water at 4ºC is called the relative density of the substance. It is a unitless quantity.
Gauge pressure : The difference between the pressures at any two points in a fluid is called gauge pressure. Mathematically it is given by ρgh, where ρ = density of the fluid, h = difference in the vertical levels of the two points. g = acceleration due to gravity.
Atmospheric pressure : The atmospheric pressure at a point is defined as the weight of a column of air of unit cross-sectional area extending from that point upto the top of the atmosphere.
Barometer : A device used to measure atmospheric pressure using a column of mercury in an inverted tube is called a barometer.
Open tube manometer : It is a device use to measure the pressure of an enclosed gas or liquid.
Streamline flow : The flow of a liquid is said to be streamlined, if each particle of the liquid passing a given point moves along the same path and has the same velocity as its predecessor had at that point.
Streamline : The path followed by a fluid particle in a steady flow is called a streamline. Two streamlines never cross each other.
Speed of efflux : The speed of outflow of a fluid through a small orifice in a tank, is called the speed of efflux veff. veff = `\sqrt{2gh}` for an open container, where h = height of the column above orifice.
Venturimeter : The Venturimeter is a device used to measure the rate of flow of a liquid through a pipe. It is an application of Bernoulli’s principle.
Dynamic lift : The upward force experienced by a body when it moves through a fluid is called dynamic lift.
Magnus effect : When a ball moving in air gets deviated from its path due to its spinning action, this effect is called Magnus effect.
Aerofoil : A streamlined shaped, solid body that is capable of generating a dynamic lift as it moves through a fluid is called an aerofoil.
Viscosity : The property of a fluid due to which its different layers offer resistance to their relative motion is called viscosity.
Coefficient of viscosity : It is defined as the ratio of shearing stress and the strain rate produced in a fluid.
Terminal velocity : The maximum constant velocity acquired by a body while falling through a viscous medium is called its terminal velocity.
Turbulence : The nature of flow of a fluid when its speed at any point in space varies rapidly and randomly with time is called turbulence.
Critical Reynold’s number : The exact value of Reynold’s number at which turbulence sets in a fluid is called Critical Reynold’s number.
Surface tension : The property of liquids due to which their free surface behaves like an elastic stretched membrane is called surface tension.
Surface tension in terms of surface energy : Surface tension is defined as the surface energy per unit area or the force per unit length acting in the plane of the interface between the plane of the liquid and any other substance.
Surface energy : The excess energy possessed by the molecules present at the surface of a liquid as compared to those present in the interiors is called surface energy.
Angle of contact : It is defined as the angle that the tangent to the liquid surface at the point of contact makes with the solid surface inside the liquid.
Capillary action : The phenomenon of a liquid rising or falling through a tube of very fine bore (capillary), is called capillary action.
For liquids, viscosity decreases with increase in temperature while for gases, viscosity increases with increase in temperature.