Law of Radioactive Disintegration | Half Life
Law of Radioactive Disintegration
According to the law of radioactive disintegration the rate of spontaneous disintegration of a radioactive element is proportional to the number of nuclei present at that time.
Mathematically, it can be written as
`\frac{dN}{dt}\infty N................(1)`
where, N is the number of atoms present at time t. Removing proportionality sign, we get
`\frac{dN}{dt}=-\lambda N............(2)`
where, λ is a constant of proportionality and is known as decay constant of the element. Negative sign indicates that as t increase N decreases.
`\frac{dN}N=-\lambda dt.............(3)`
Integrating both sides, we have
`\int\frac{dN}N=-\lambda\int dt`
`\log_e(N)=-\lambda t+C.............(4)`
where C is constant of integration and is evaluated by the fact that at t = 0, number of atoms of the radioactive element is N0. Using this condition, we get
`C=\log_e(N_0).................(5)`
Substituting this value of C in Eq. (5), we get
`\log_e(N)=-\lambda t+\log_e(N_0)`
`\log_e(N)-\log_e(N_0)=-\lambda t`
Thus,
`N=N_0e^{-\lambda t}.................(6)`
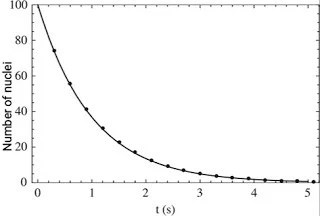 |
| Exponential decay curve |
Units of Activity
The SI unit of activity is named after Becquerel. Active of a radioactive sample is said to be 1 becquerel if rate of decay is 1 nucleus per second.
Therefore,
becquerel = 1 Bq = 1 decay/sec
An older unit Curie (Ci) is still commonly used to measure activity.
Therefore,
1 curie = 1 Ci = 3.7 × `10^{10}` decay/sec = 3.7 × `10^{10}` Bq
Yet, another unit of activity of radioactive sample is rutherford (Rd) and is defined as :
1 rutherford = 1 Rd = `10^{10}` decay/sec = `10^{10}` Bq
Half-life
Half-life is the time at which the activity of sample has been reduced to one-half of its initial value.
If N0 is the initial number of radioactive nuclei present, then in one half-life this number will reduce to N0/2. Therefore,
`N=\frac{N_0}2`
substituting N in Eq. (6), we get
`\frac{N_0}2=N_0e^{-\lambda t_{1/2}}`
`\1/2=e^{-\lambda t_{1/2}}`
`e^{\lambda t_{1/2}}=2`
Taking natural log on both sides,
`\lambda t_{1/2}=\log_e2`
`t_{1/2}=\frac{2.303\log_{10}\2}\lambda`
`[ \log_ex=2.303\log_{10}x\ ]`
`t_{1/2}=\frac{0.693}\lambda`
Therefore, half-life of a radioactive material depends upon the disintegration constant. The larger the value of disintegration constant, smaller is the half-life. Half-life of a radioactive material is its intrinsic property it cannot be altered by any physical or chemical means.
Read also
Thank you for visiting on my this web portal. Here, I provide short and to the point notes on physical science so you may go through the home page for the other topics of your lesson.

