Electromagnetic Induction Class 12 notes Physics Chapter 6
Introduction
Imagine a world where there are no electric lights, no trains, no telephones, and no personal computers. It was life before the discovery of electromagnetic induction. A Revolutionary invention as a result of the experiments of Michael Faraday and Joseph Henry.
In this chapter, we will study the experiments of electromagnetic induction and their applications.
The Experiments of Faraday and Henry
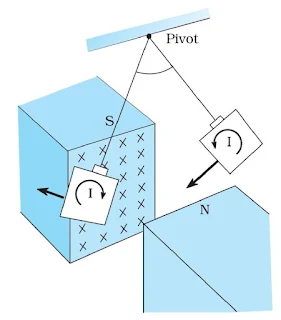
The figure shows a coil C1 connected to a galvanometer G. When the North-pole of a bar magnet is pushed towards the coil, the pointer in the galvanometer deflects, indicating the presence of electric current in the coil. The galvanometer does not show any deflection when the magnet is held stationary. When the magnet is pulled away from the coil, the galvanometer shows deflection in the opposite direction, which indicates a reversal of the current’s direction.
Moreover, when the South-pole of the bar magnet is moved towards or away from the coil, the deflections in the galvanometer are opposite to that observed with the North-pole for similar movements. Further, the deflection is found to be larger when the magnet is pushed towards or pulled away from the coil faster. Instead, when the bar magnet is held fixed and the coil C1 is moved towards or away from the magnet, the same effects are observed. It shows that it is the relative motion between the magnet and the coil that is responsible for the generation of electric current in the coil.
Recommended Books
- NCERT Textbook For Class 12 Physics Part 1 & 2
- CBSE All In One Physics Class 12 2022-23 Edition
- Oswaal CBSE Chapterwise Question Bank Class 12 Physics Book
- Modern's abc Plus of Physics for Class-12 (Part I & II)
Read also: Alternating Current Class 12 Physics Notes Chapter 7
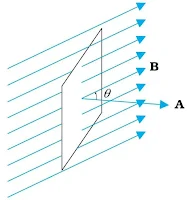
Magnetic Flux
Like electric flux, magnetic flux is proportional to the number of magnetic field lines passing through a surface. It is denoted by ΦB. It is a scalar quantity.
Mathematically, `\phi_{B}=\vec{B}\vec{A}=BAcos\theta`
SI unit of magnetic flux is weber (Wb) (1Wb = 1 tesla-m2). C.G.S. unit of magnetic flux is maxwell. The dimensional formula of magnetic flux is [ML2T-2A-1]
Faraday’s Law of Induction
(i) First law
According to this law, "The magnitude of the induced emf in a closed loop is equal to the time rate of change of magnetic flux through the loop."
`\epsilon=\frac{-d\phi}{dt}`
In case of a coil of N turns, induced emf
`\epsilon=-N\frac{d\phi}{dt}`
(ii) Second Law (Lenz's Law)
According to this law, the induced current is in such a direction, so as to oppose its cause. i.e. induced current opposes the change in flux.
Read also: General Principles and Processes of Isolation of Elements Class 12 Chemistry Notes Chapter 6
Lenz’s Law and Conservation of Energy
Lenz's law is in accordance with the law of conservation of energy. As the induced current opposes the change in flux, work has to be done against the opposition offered by the induced current in changing the flux. The work done appears as electrical energy in the loop.
Induced Electric Field
An electric field is induced in any region of space in which a magnetic field is changing with time. The induced electric field and magnetic field are at right angles to each other.
Consider a particle of charge q0 moving around the ring in a circular path. The work done by the induced electric field in one revolution is W = q0ε, where ε is the induced emf.
Also work done
`W=\int\vec{F}.\vec{dl}`
`W=q_{0}\int\vec{E}.\vec{dl}`
`q_{0}\epsilon=q_{0}\int\vec{E}.\vec{dl}`
`\epsilon=\int\vec{E}.\vec{dl}`
By Faraday's law
`\epsilon=\frac{-d\phi_B}{dt}`
`\therefore\int\vec{E}.\vec{dl}=\frac{-d\phi_B}{dt}`
Read also: Conceptual Questions for Class 12 Physics Chapter 6 Electromagnetic Induction
Eddy Current
Even when bulk pieces of conductors are subjected to changing magnetic flux, induced currents are produced in them, these currents are called eddy currents.
Eddy currents are undesirable since they heat up the core and dissipate electrical energy in the form of heat. Eddy currents are minimized by using laminations of metal to make a metal core. This arrangement reduces the strength of the eddy currents.
Eddy currents are used to advantage in certain applications like:
Magnetic braking in trains: Strong electromagnets are situated above the rails in some electrically powered trains. When the electromagnets are activated, the eddy currents induced in the rails oppose the motion of the train.
Electromagnetic damping: Certain galvanometers have a fixed core made of non-magnetic metallic material. When the coil oscillates, the eddy currents generated in the core oppose the motion and bring the coil to rest quickly.
Induction furnace: Induction furnace can be used to produce high temperatures. A high-frequency alternating current is passed through a coil that surrounds the metals to be melted. The eddy currents generated in the metals produce high temperatures sufficient to melt them.
Electric power meters: The shiny metal disc in the electric power meter rotates due to the eddy currents. Electric currents are induced in the disc by magnetic fields produced by sinusoidally varying currents in a coil.
Self Inductance
Self-inductance is the property of a coil, by which an induced emf is developed in itself due to a change in the strength of the current flowing through the coil itself.
Let a current 'i' flows through the inductor. Due to this current, a flux Φ is linked with it such that
`\phi\propto i`
`\phi=Li`
L is called the inductance of self-inductance of the coil.
The induced emf is given by
`\epsilon=\frac{-d\phi}{dt}`
`\epsilon=\frac{-Ldi}{dt}`
SI unit of inductance is henry (H).
(i). Self Inductance of a solenoid
Let a current 'i' be flowing through the solenoid. There is a uniform magnetic field B = μ0ni in its core. The total flux linked with the solenoid is
`\phi=(\mu_{0}ni)\times A\times N`
`\phi=\mu_{0}ni\times \pi r^2\times (nl)`
`\phi=\mu_{0}n^{2}\pi r^{2}l\times i`
`L=\mu_{0}n^{2}\pi r^{2}l` ......[`\phi=Li`]
(ii). Energy Stored in an Inductor
Like a capacitor stores energy in the form of an electric field, an inductor stores energy in the form of a magnetic field. Let a current 'i' be flowing through an inductor of inductance L. As the current increase a rate
`V_{AB}=L\frac{di}{dt}`
`Power=Vi`
`\frac{dW}{dt}=(L\frac{di}{dt})i`
`dW=Lidi`
`W=\frac{1}{2}Li^2`
Mutual Inductance
The phenomenon by which an induced emf is produced in one coil due to a change in the strength of the current flowing through another coil is called mutual induction.
When a current i flows through one of the coils, a flux Φ is linked with another coil such that
`\phi\propto i`
`\phi=Mi`
The constant M is called the coefficient of mutual inductance between the coils.
`\epsilon=\frac{-d\phi}{dt}`
`\epsilon=\frac{-Mdi}{dt}` .....[`\phi=Mi`]
SI unit of mutual inductance is henry (H).
AC Generator
An ac generator converts mechanical energy into electrical energy.
It consists of a coil mounted on a rotor shaft. The axis of rotation of the coil is perpendicular to the direction of the magnetic field. The coil (called the armature) is mechanically rotated in the uniform magnetic field by some external means. The rotation of the coil causes the magnetic flux through it to change, so an emf is induced in the coil. The ends of the coil are connected to an external circuit by means of slip rings and brushes.
When the coil is rotated with a constant angular speed ω, the angle θ between the magnetic field vector B and the area vector A of the coil at any instant t is θ = ωt. As a result, the effective area of the coil exposed to the magnetic field lines changes with time, and the flux at any time t is
`\phi_{B}=BA cos\theta`
`\phi_{B}=BA cosωt`
From Faraday’s law, the induced emf for the rotating coil of N turns is, then,
`\epsilon=-N\frac{d\phi_{B}}{dt}`
`\epsilon=-NBA\frac{d}{dt}(cos\omega t)`
Thus, the instantaneous value of the emf is
`\epsilon=NBA\omega sin\omega t`
If we denote NBAω as ε0,
`\epsilon=\epsilon_{0}sin\omega t`
The direction of the current changes periodically and therefore the current is called alternating current (ac).
Summary
Electricity and magnetism are interrelated.
Scientists Oersted and ampere demonstrated experimentally that moving charges (currents) produce a magnetic field.
In a closed circuit, electric currents are induced so as to oppose the changing magnetic flux.
Lenz’s law is in accordance with the law of conservation of energy.
The motional emf can be discussed independently from Faraday’s law by using Lorentz force on moving charges.
Moving charges in a static field and static charges in a time-varying field seem to be the symmetric situation for Faraday’s law.
The motion of a copper plate is damped when it is allowed to oscillate between the magnetic pole pieces, this is because eddy current loops are induced in the bulk of the conductor.
Eddy current losses can be minimized by having slot cuts in the bulk of the conductor, thereby cutting the eddy current loops.
The magnetic potential energy of the inductor at any instant depends upon the strength of the current flowing in the inductor at that instant. It does not depend upon the manner in which the current is changing.
Magnetic flux linkage through a surface is proportional to the number of field lines passing through it.
The induced emf is equal to the negative of the time rate of change of magnetic flux.
The self-inductance is numerically equal to the magnetic flux when the unit current is flowing in the coil.
The self-inductance of a coil is numerically equal to the emf induced across the ends of the coil when the rate of change of current is 1 A/s.
An induced charge is numerically equal to the change in magnetic flux if the resistance of the circuit is unity.
Magnetic flux is a scalar quantity as it is the scalar product of the magnetic field and area (vector).
The mutual inductance of two coils is numerically equal to emf induced across one coil when the rate of change of current in the other coil is 1 A/s.