Waves Class 11 notes Physics Chapter 15
Introduction
In this chapter, we shall discuss the type of propagation of waves through different media, and the factors affecting the speed of waves in them. We will also discuss the superposition of waves and Doppler’s effect in sound.
Most of us experience the phenomenon of wave propagation when we drop a stone in a pond of still water. These waves move outwards in expanding circles until they reach the shore. It seems as if the water is moving outward from the point of disturbance.
Thus we can say that energy is transferred but there is no transfer of medium. Such a pattern in which there is no actual transfer of matter as a whole but energy is transmitted from one part of a medium to another part is called wave.
Transverse and Longitudinal Waves
(i). Transverse waves
Transverse waves are the waves in which the constituents of the medium oscillate perpendicular to the direction of wave propagation.
If we give an upward jerk to one end of a long rope that has its opposite end fixed, a single wave pulse is formed and travels along the rope with a fixed speed.
(ii). Longitudinal waves
Longitudinal waves are the waves in which the constituents of the medium oscillate along the direction of wave propagation.
Displacement Relation in a Progressive Wave
A traveling wave is also referred as a progressive wave. It may be transverse or longitudinal. We consider a transverse wave so that if it travels along positive x-axis, the constituent particles of the medium vibrate along y-axis, about their mean positions. In general, sinusoidal shape can be described by sine function or cosine function.
At time t, the displacement y of the element located at position x is given by
y(x, t) = a sin(kx – ωt + φ)
where y(x, t) → Displacement of the medium particles from their mean positions
a → Amplitude of a wave
ω → Angular frequency of the wave
k → Angular wave number
φ → Initial phase angle
Recommended Books
- NCERT Textbook For Class 11 Physics Part 1 & 2
- CBSE All In One Physics Class 11 2022-23 Edition
- Oswaal CBSE Chapterwise Question Bank Class 11 Physics Book
- Modern's abc Plus of Physics for Class-11 (Part I & II)
Read also: Electric Charges and Fields Class 12 Physics Notes Chpter 1
Some Important Terms
(i). Amplitude
The maximum displacement of the constituents of the medium from their equilibrium position is called amplitude of the wave.
(ii). Phase
Phase of a wave is the argument of the sine function. Phase determines the displacement of the wave at any position and at any instant.
(iii). Crest
It is the point of maximum positive displacement on a wave. The peak of a sinusoidal wave represents a crest.
(iv). Trough
It is the point of maximum negative displacement on a wave.
(v). Time period
Time period of oscillation of the wave is the time it takes for an element of the medium to complete one full oscillation.
`T=\frac{2\pi}{ω}`
Read also: Some Basic Concepts of Chemistry Class 11 Notes Chapter 1
(vi). Wavelength
Wavelength is the minimum distance between two points having the same phase at a given time. It is usually denoted by λ.
`λ=\frac{2\pi}{k}`
Where k is the angular wave number or propagation constant.
(vii). Frequency
The frequency 'ν' of the wave is the number of oscillations per second. It is denoted by the symbol ‘ν’. The SI unit of frequency is hertz (Hz).
`ν=\frac{1}{T}=\frac{ω}{2\pi}`
The Speed of a Traveling Wave
If we focus on a particular point on the wave and observe the motion of this point in time, we can determine the speed of a traveling wave.
Read also: Conceptual Questions for Class 11 Physics Chapter 15 Waves
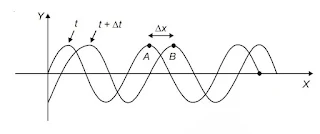
Here in the figure we have two snapshots of a single traveling wave taken in a small interval Δt. The entire wave moves through a distance Δx in interval Δt. The wave speed can be calculated using the relation v = Δx/Δt.
Let us consider a crest shown by point A in the figure. As the time changes, the position of the crest changes from A to B. Since the phase remains constant
∴ kx – ωt = k(x + Δx) – ω(t + Δt)
⇒ kx – ωt = kx + kΔx – ωt – ωΔt
kΔx = ωΔt
`\frac{Δx}{Δt}=\frac{ω}{k}`
Taking Δx and Δt very small,
∴ `v=\frac{dx}{dt}=\frac{ω}{k}`
Hence, the speed of the wave is
⇒ `v=\frac{ω}{k}`
Also we have, `ω=\frac{2\pi}{T} & k=\frac{2\pi}{λ}`
`v=\frac{λ}{T}` or `v=fλ`
(i). Speed of a transverse wave on stretched string
The speed of a mechanical wave depends on the inertial and elastic properties of the medium. It is inversely related to the inertial property and directly to the elastic property of medium. In case of a stretched string inertial property is its linear mass density (μ). Further, we cannot send a wave along a string unless the string is under a tension. Therefore, we can associate the tension with the elasticity of the string.
Speed of transverse waves on a stretched string is given by
`v=\sqrt{\frac{T}{μ}}`
(ii). Speed of a longitudinal wave
In longitudinal waves, the constituents of the medium oscillate along the direction of wave propagation. The speed of a longitudinal wave also depends on inertial property as well as elastic property of the medium. The longitudinal waves, such as sound, travel in the form of compressions and rarefactions. Therefore, bulk modulus of the medium can be associated with the elastic property of the medium. Further inertial property relevant for the propagation of these waves is the mass density (ρ), of the medium.
Speed of longitudinal waves
`v=\sqrt{\frac{B}{ρ}}`
In case of a linear medium like a solid rod the relevant modulus of elasticity is Young’s modulus (Y). Therefore, in case of solids, velocity of longitudinal wave is given by
`v=\sqrt{\frac{Y}{ρ}}`
Note: The speed of sound is greater in solids and liquids than in gases even though they are denser than gases. This happens because they are much more difficult to compress than gases and so have much higher values of bulk modulus.
(iii). Speed of sound in gases
Newton assumed that when sound waves propagate through a gas, the change in pressure and volume of the gas are isothermal. The amount of heat produced during compressions is lost to the surroundings and the amount of heat lost during rarefactions is gained from the surroundings. Therefore, the temperature of the gas remains constant.
The speed of longitudinal waves in an ideal gas is
`v=\sqrt{\frac{P}{ρ}}`
This relation is known as Newton’s formula.
(iv). Laplace correction
Newton assumed that the pressure variations in a medium during propagation of sound are isothermal. Laplace pointed out that the pressure variations in the gases when sound propagates are so fast that the heat does get enough time to flow to surroundings or from surroundings to keep the temperature constant. Therefore, the variations are adiabatic and not isothermal.
The speed of sound in a gas is
`v=\sqrt{\frac{γP}{ρ}}`
This value of the speed of sound matches with the speed of sound measured experimentally.
The Principle of Superposition of Waves
Whenever two wave pulses traveling in opposite directions cross each other, they retain their individual identities. However at the instant, they overlap each other, the wave pattern is different from the individual pulses. The resultant displacement, at the instant they overlap, is the algebraic sum of the displacement due to each pulse.
Thus we can say that each pulse moves as if others are not present. The net displacement of the constituents of the medium is an algebraic sum of the two interfering pulses. This is called the principle of superposition of waves.
Reflection and Transmission of Waves
When a progressive wave, like a transverse wave travelling along a stretched string arrives at a rigid boundary, the wave gets reflected. The reflected wave suffers a phase change of 180° on reflection. At the rigid boundary, disturbance must have zero displacement all the time. By the principle of superposition, this could be possible only when the two waves (the incident and the reflected waves) have a phase difference of 180° or π radian.
If we apply Newton’s 3rd law, the arriving wave exerts a force on the rigid boundary. The reaction to this force, exerted by the rigid boundary on the string ‘Kicks back’ on the string and sets up a reflected pulse with a phase difference of π radian. Thus, a crest is reflected as a trough.
The phenomenon of echo is an example of reflection of sound by a rigid boundary.
Standing or Stationary Waves
When a travelling wave in one direction will get reflected at one end, which in turn will travel and get reflected from the other end. This will go on until there is a steady wave pattern set up on the string. Such wave patterns are called standing waves or stationary waves.
The points, where the oscillation amplitude is zero are called displacement nodes and the points where the displacement amplitude is maximum are called displacement antinodes. Thus, the particles at nodes do not move at all, hence prohibiting any flow of energy through them.
Beats
When two harmonic sound waves of equal amplitude but slightly different frequencies superpose, the resultant wave looks like a single sinusoidal wave with a varying amplitude that goes from maximum to zero and back. The amplitude variation causes the variation of intensity called beats. The frequency with which the amplitude rises and falls is called the beat frequency and is equal to the difference in frequencies of the two waves. The rise and fall of the intensity of sound is called waxing and waning.
Doppler Effect
Whenever there is a relative motion between the source of sound and an observer, the frequency of sound received or heard by the observer is different from the frequency of sound produced by the source. This is called Doppler effect.
Doppler effect can be observed when
The source is moving but the observer is stationary.
The observer is moving but the source is stationary.
Both the source and observer are moving.
(i). Source Moving : Observer Stationary
Let us consider a source of sound producing a wave of angular frequency ω, velocity v and time period T0, moving with velocity vs. As a convention we have taken the direction from the observer to the source as positive.
`ν=ν_{0}(\frac{ν}{ν+ν_s})`
For a source approaching the observer
`ν=ν_{0}(\frac{ν}{ν-ν_s})`
(ii). Observer Moving : Source Stationary
Let us consider a source of sound producing a wave of angular frequency ω, velocity v and time period T0, to be at rest. While an observer initially at O1 is moving with velocity vs towards the source.
`ν=ν_{0}(\frac{ν+ν_0}{ν})`
If the observer moves away from the source,
`ν=ν_{0}(\frac{ν-ν_0}{ν})`
(iii). Both Source and Observer Moving
Let us consider that both the source and observer are moving with velocity vs and v0 respectively. The source emits a wave of angular frequency ω, velocity v and time period T0.
The observed frequency is given by
`ν=ν_{0}(\frac{ν+ν_0}{ν+ν_s})`
Summary
Wave : It is a kind of disturbance that travels through a medium, accompanied by the transfer of energy.
Mechanical wave : It is a wave that requires a material medium for its propagation.
Electromagnetic wave : It is a wave that does not necessarily require a material medium for propagation. Electromagnetic wave can travel through vacuum.
Transverse wave : It is a wave in which the constituents of the medium oscillate perpendicular to the direction of wave propagation.
Longitudinal wave : It is a wave in which the constituents of medium oscillate along the direction of wave propagation.
Crest : It is the point of maximum positive displacement in a transverse wave. Trough : It is the point of maximum negative displacement in a transverse wave.
Amplitude : It is the maximum displacement of the constituents of the medium from their equilibrium position. It is usually denoted by ‘a’ or ‘A’.
Wavelength : It is the minimum distance between any two points on a wave having the same phase. Or, it is the distance between the two consecutive crests or troughs in a wave. It is denoted by λ.
Time period : The time period of oscillation of a wave is the time it takes for an element to complete one full oscillation. It is denoted by T.
Frequency : It is the number of complete wavelengths traversed by the wave in one second. It is denoted by ν or f.
Phase : The phase of an oscillating particle at any instant denotes the position and the direction of motion of the particle at that instant.
Phase difference : It is the difference in the phases of two particles of the medium at the same instant. Or the difference in the phases of a single particle at different instants.
Interference of waves : It is the superposition of two waves of same frequency, with constant phase difference.
Constructive interference : It is the phenomenon of superimposition of two waves of same frequency, with zero phase difference.
Destructive interference : It is the phenomenon of superimposition of two waves of same frequency, with a phase difference of odd multiple of π radian.
Stationary wave/ standing waves : When two waves of equal amplitude and frequency, moving with same speed in opposite directions, superimpose, the resultant wave is called of stationary or standing wave.
Node : It is a point along a standing wave, where the wave has zero amplitude.
Antinode : It is a point along a standing wave, where the wave has maximum amplitude.
Beats : The audibly distinct waxing and waning of the intensity of sound, which are produced, when two sound waves of slightly different frequencies and comparable amplitudes are superposed, are called beats.