Oscillations Class 11 notes Physics Chapter 14
Introduction
In this chapter, we shall study simple harmonic motion (SHM), periodic motion of pendulum and spring mass system, damped and forced oscillations and many more interesting topics.
In our daily life we come across various kinds of motions. The motion is repeated after a certain interval of time is called periodic motion. The study of oscillatory motion is basic to physics. In musical instruments, like the sitar, the guitar or the violin, we come across vibrating strings that produce pleasing sounds. The vibrations of air molecules make the propagation of sound possible.
Periodic and Oscillatory Motions
(i). Periodic Motions
Periodic motion is defined as that motion which repeats itself after equal intervals of time. The interval of time is called the time period of periodic motion. Ex- Rotational motion of Earth about its rotational axis and its time period is 24 hour.
(ii). Oscillatory Motions
Oscillatory or vibratory motion is defined as a periodic and bounded motion of a body about a fixed point. Ex- motion of the pendulum of a wall clock, motion of the bob of a simple pendulum displaced once from its mean position.
Period and Frequency
(i). Period
Period is the smallest interval of time after which the motion is repeated. It is denoted by the symbol T. Its SI unit is second.
(ii). Frequency
Frequency is defined as the number of oscillations per unit time. It is the reciprocal of time period T. It is represented by the symbol f. Its SI unit is hertz (Hz).
The relation between f and T is
`f\propto\frac{1}{T}`
Recommended Books
- NCERT Textbook For Class 11 Physics Part 1 & 2
- CBSE All In One Physics Class 11 2022-23 Edition
- Oswaal CBSE Chapterwise Question Bank Class 11 Physics Book
- Modern's abc Plus of Physics for Class-11 (Part I & II)
Read also: Waves Class 11 Physics Notes Chapter 15
Displacement
The angle with the vertical as a function of time is the displacement variable. Consider a block attached to a spring, whose other end is fixed to a rigid wall. Here, it is convenient to measure displacement of the body from its equilibrium position.
Simple Harmonic Motion
Simple harmonic motion is a special type of periodic oscillatory motion in which
The particle oscillates on a straight line.
The acceleration of the particle is always directed towards a fixed point on the line.
The magnitude of acceleration is proportional to the displacement of the particle.
Read also: Environmental Chemistry Class 11 Notes Chemistry Chapter 14
Velocity and Acceleration in Simple Harmonic Motion
The speed v of a particle in uniform circular motion is, its angular speed ω times the radius of the circle A.
The direction of velocity v at a time t is along the tangent to the circle at the point where the particle is located at that instant. From the geometry of the given figure, it is clear that the velocity, of the projection particle P' at time t is
`v(t)=-\omega A sin(\omega t+\phi)`
Where the –ve sign shows that direction of v(t) is opposite to the +ve direction of x-axis.
The instantaneous acceleration of the projection of particle P' is then
`a(t)=–\omega ^{2} A cos(\omega t + \phi)`
Read also: Conceptual Questions for Class 11 Physics Chapter 14 Oscillations
Energy in Simple Harmonic Motion
KE and PE of a particle in SHM vary between zero and their maximum values. The velocity of a particle executing SHM is zero at the extreme positions. So, the kinetic energy (K) of such a particle is
`K=\frac{1}{2}mv^2`
`K=\frac{1}{2}m\omega^{2}A^{2}sin^2(\omega t+\phi)`
`K=\frac{1}{2}kA^{2}sin^2(\omega t+\phi)`
This is also a periodic function of time, being zero when the displacement is maximum and minimum when the particle is at the mean position.
The spring force, F = –kx is a conservative force, with associated potential energy.
`U=\frac{1}{2}kx^2`
So, the P.E. of a particle executing SHM is,
`U=\frac{1}{2}kA^2cos^2(\omega t+\phi)`
So, PE of a particle executing SHM is also periodic, with period T/2, being zero at the mean position and maximum at the extreme displacements.
The total energy, E, of the system is
E = U + K
`E=\frac{1}{2}kA^2cos^2(\omega t+\phi)+\frac{1}{2}kA^2sin^2(\omega t+\phi)`
`E=\frac{1}{2}kA^2[cos^2(\omega t+\phi)+sin^2(\omega t+\phi)]`
`E=\frac{1}{2}kA^2`
The total mechanical energy of a harmonic oscillator is thus independent of time as expected for motion under any conservative force.
Some Syetem Executing S.H.M.
(i). Oscillations due to a Spring
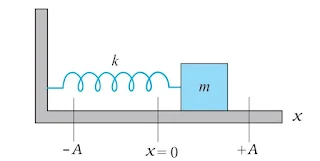
The simplest example of SHM is the small oscillations of a block of mass m fixed to a spring, which is fixed to a rigid wall as shown in figure.
In the figure A linear SHM consisting of a block of mass m is attached to a spring. The block moves over a frictionless surface. The block, when pulled or pushed and released, executes SHM. At any time t, the displacement from the mean position is x, and the restoring force F acting on the block is
F(x) = –kx
The constant of proportionality, k is called the spring constant. Its value is governed by the elastic properties of the spring. A soft spring has small value of k and a stiff spring has large value of k.
Angular friquency of the oscillator is given by,
`ω=\sqrt{k/m}`
Time period of the oscillator is given by
`T=2\pi\sqrt{m/k}`
(ii). The Simple Pendulum
Make a simple pendulum by tying a piece of stone to a long unstretchable thread, approximately 100 cm long, suspend it from a suitable support so that it is free to oscillate. Displace the stone to one side by small distance and let it go. The stone executes to and fro motion (periodic motion) with a period of about 2 seconds.
Consider a simple pendulum. A small bob of mass m is tied to an inextensible massless string of length L. The other end of the string is fixed to a support on the ceiling. The bob oscillates in a plane about the vertical line through the support. Let θ be the angle which the string makes with the vertical. Here θ = 0 when the bob is at the mean position. The two forces acting on the bob are
The tension T along the string and
The vertical force due to gravity (mg).
The formula for time period of a simple pendulum is given by,
`T=2\pi\sqrt{L/g}`
Damped Simple Harmonic Motion
When a simple harmonic system oscillates with a decreasing amplitude with time, its oscillations are called damped simple harmonic oscillations. The angular frequency of the damped oscillator given by
`ω=\sqrt{\frac{k}{m}-\frac{b^2}{4m^2}}`
Where b is a damping constant.
Forced Oscillations and Resonance
When a system (like a simple pendulum is displaced from its equilibrium position and released, it oscillates with its natural frequency ω and the oscillations are called free oscillations. They die out eventually due to damping forces. However, they can be maintained by an external agency. These are called forced or driven oscillations.
The phenomenon of increase in amplitude when the driving force is close to the natural frequency of the oscillator is called resonance. You can swing to greater heights if the rhythm of pushing against the ground is synchronised with the natural frequency of the swing.
Summary
Periodic Motion : When a body repeats its motion continuously on a definite path in a definite interval of time, its motion is called periodic motion.
Oscillatory or Vibratory Motion : If a body moves to and fro about a point on the same path, then the motion of the body is an oscillatory motion.
Simple Harmonic Motion : When a particle oscillates on a path, the acceleration of particle is always directed towards a fixed point on its path and its magnitude is proportional to the displacement of the particle from fixed point, then the motion of the particle is simple harmonic motion.
Time Period : The smallest definite interval of time after which the motion in repeated, is called time period of the motion.
Frequency : The number of oscillations per unit time is called frequency of oscillation.
When a particle executing SHM passes through its equilibrium position, its velocity is maximum and acceleration is minimum.
The total mechanical energy of a harmonic oscillator is constant.
The maximum value of time period of a simple pendulum is approximately 84.6 minute.
In the ideal case of zero damping, the amplitude of SHM at resonance is infinite. This is no problem as all real systems have some damping, however small.
Under forced oscillations, the phase of harmonic motion of the particle differs from the phase of the driving force.